[:pb]Vimos na Parte 1 dessa série que existe uma fórmula para o cálculo de tamanho de amostra para CEP, e na Parte 2 começamos a discutí-la e a colocar valores para os parâmetros da mesma. Agora vamos ver como proceder em um caso genérico, em que você entra com todas as informações para calcular o tamanho de amostra necessário. Essa discussão é um pouco mais técnica, mas vou colocá-la de forma simples (pelo menos vou tentar).

Comecemos da fórmula mais uma vez:

z_α/2 e z_β vão determinar a probabilidade de ocorrer um alarme falso e a capacidade de detectar mudanças no processo. É intuitivo que quanto menor a amostra medida, menos informação temos sobre o processo, e portanto maior a probabilidade de cometermos erros de avaliação. Lembre-se sempre que o objetivo de uma carta de controle é detectar se a média ou o desvio padrão de um processo mudaram em relação aos seus valores históricos (que definem os limites de controle). Tudo que estamos vendo aqui aplica-se à carta de médias apenas, mas para a carta de variação (amplitude ou desvio padrão) as ideias são as mesmas.

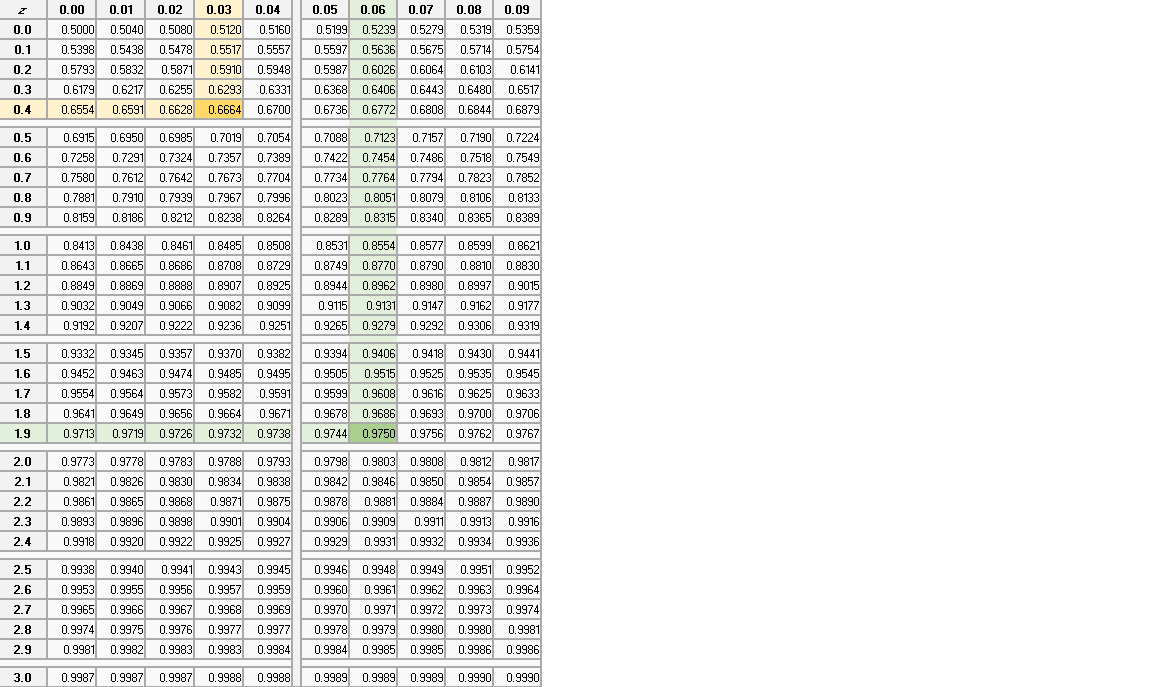
z_α/2 pode ser obtido de uma tabela de probabilidade normal (veja abaixo), definido o valor de α. α é o percentual tolerado de alarmes falsos, que é quando temos um alarme mesmo sem mudança no processo. Sugeri uma probabilidade de 5% de alarme falso. Usamos metade de α (2,5%, ou 0,025), porque existe a chance de erro da média para cima ou para baixo da média do processo; e procuramos 1-α/2 (0,975) na tabela de probabilidade abaixo. O valor que procuramos está destacado em verde, e temos um z de 1,96.

z_β também vem da tabela de probabilidade normal, definido o valor de β. β é o risco tolerado de não detectar alarmes, que é quando temos uma variação da média superior a δ, mas a carta não acusa isso. O valor de 1-β é chamado de poder estatístico da carta de controle (representado por π), e informa a probabilidade de um ponto ficar fora dos limites da carta de controle quando a mudança da média é igual a δ. Sugeri um valor de 33% para π, e portanto temos que procurar o valor de 0,667 na tabela abaixo. O valor aproximado está destacado em laranja (usei na fórmula o valor de 0,431). Lembro que se π=33%, dois terços dos pontos gerados depois da mudança de δ na média do processo ainda ficarão dentro dos limites de controle.

Calculando (z_α/2 + z_β)², temos (1,96 + 0,431)² = 5.717. Daí saiu a constante sugerida na fórmula.

Para este post já chega, parabéns se você conseguiu chegar até aqui. No próximo post vamos discutir um pouco o que é o Comprimento Médio da Corrida (quantos pontos até obtermos um alarme), e apresentar exemplos para cálculo de tamanho de amostra. Até lá!

 [:]