[:pb]

O que considerar no momento de definir estratégias de amostragens? Qual a melhor maneira de organizar os dados em subgrupos? Parecem perguntas simples, porém é fundamental conhecer e entender suas respostas para que as análises gráficas de fato sejam válidas. É sobre isso que vamos tratar neste post, que é o tema apresentado no Terceiro Fundamento de Shewhart para os Gráficos de Controle.

Fundamento Três: Amostragem e Subgrupo Racional

Amostragem Racional

Amostras racionais são tomadas levando em consideração a forma como o processo é medido e o quê, onde e quando é medido. Seguem algumas perguntas para ajudar a definir uma amostragem racional:

• Quem coletará os dados?

Avalie as habilidades do operador para coletar dados. Quanto tempo o operador dispõe? O operador tem recursos adequados para coletar os dados?

• O que será medido?

Foque em características chave. Sempre lembre que medir custa dinheiro! Devemos focar nas características que são críticas para controlar o processo.

• Onde a amostra será retirada?

A amostra deve ser tomada em um ponto do processo que permita que os dados sejam usados para o controle do processo.

• Quando a amostra será retirada do processo?

As amostras devem ser tomadas com frequência suficiente para refletir as mudanças do processo.

• Porque estamos medindo?

As informações coletadas precisam possibilitar a tomada de ações no processo. Os dados serão usados para controle do processo ou controle do produto?

• Como os dados serão coletados?

Deve ser estabelecido um procedimento padrão para a coleta de dados. Instrumentos e operadores diferentes não devem interferir nos resultados obtidos.

• Quantos itens serão medidos?

As amostras devem ser aleatórias e representativas. O tamanho da amostra deve ser suficiente para o controle do processo, sem ser grande demais, causando grandes custos, perdas de tempo ou produtividade.

Subgrupo Racional

Uma vez que as amostragens foram realizadas de forma racional, os dados obtidos também devem ser agrupados de forma racional. Este agrupamento é chamado de subgrupo, ou seja, é um conjunto de indivíduos registrados como um ponto no gráfico. Subgrupo racional é aquele onde há baixa probabilidade de apresentar variações por causas atribuíveis dentro do subgrupo. Existem alguns princípios para agrupar subgrupos que devem ser usados na construção de Gráficos de Controle, são eles:

• Nunca agrupe coisas diferentes em um subgrupo:

Não misture informações de processos diferentes, produtos diferentes, momentos diferentes… Informações de fontes distintas precisam ser avaliadas individualmente, do contrário, informações importantes podem ser mascaradas e conclusões errôneas podem ser tomadas.

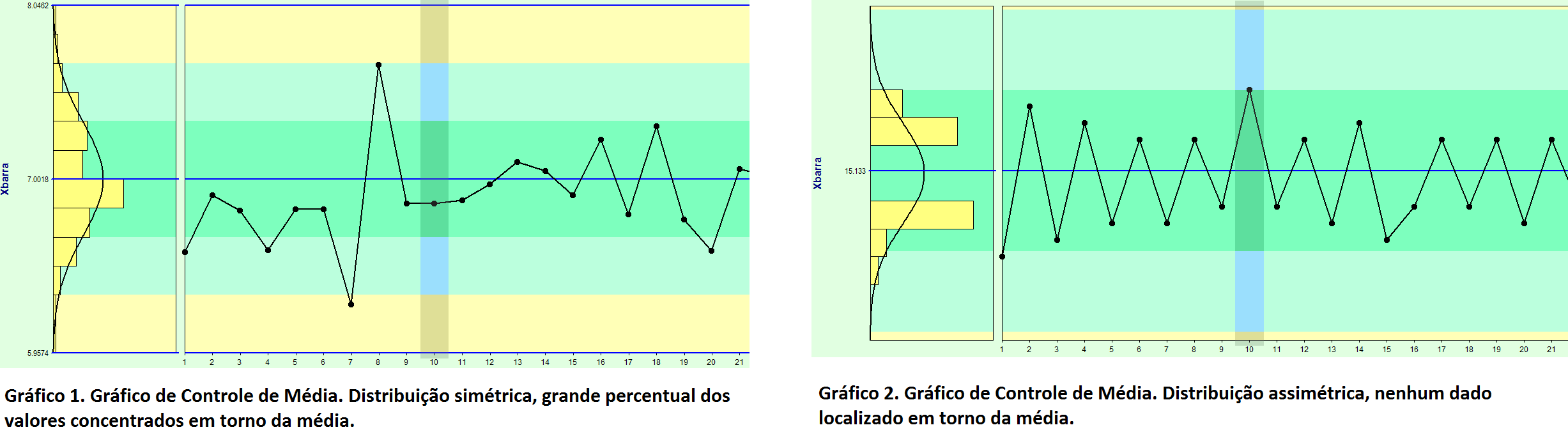
Por exemplo, produtos de diferentes linhas de produção não devem ser misturados em um subgrupo. No Gráfico 1, podemos ver que a distribuição é simétrica, não indica a mistura de informações diferentes. Já no Gráfico 2, vemos que a distribuição dos dados se acumula afastada da média do processo, indicando uma mistura de informação (por exemplo, a saída de duas linhas diferentes). Neste caso, os dados devem ser analisados separadamente, para que as informações transpareçam a realidade da produção.

• Minimize a variação em cada subgrupo

A variação dentro de cada subgrupo interfere diretamente nos limites de controle. Quando você minimiza a variação dentro do subgrupo você estará criando um Gráfico de Controle que será sensível aos sinais do processo (causas atribuíveis – grandes variações), pois somente os ruídos (causas aleatórias – pequenas variações) serão considerados para definir a variação do processo.

Se somente variações aleatórias existirem nos subgrupos, quaisquer diferenças entre ou dentro dos subgrupos serão atribuídas a causas atribuíveis.

• Maximize a oportunidade de variação entre os subgrupos

Se existe a possibilidade de interferências, certifique-se de que elas estejam em subgrupos diferentes. O gráfico de média analisa as diferenças entre os subgrupos. Ele usa a variação dentro do subgrupo para saber quanta variação deve ser ignorada entre os subgrupos e assim detectar as causas atribuíveis atuando.

• Faça média de coisas similares, não de coisas diferentes

O objetivo de utilizar a média de subgrupos é agrupar coisas onde somente ruídos (variações inerentes ao processo) atuam para que seja fácil identificar quando um sinal está atuando no processo.

• Utilize o gráfico adequado para o tipo de dado

Se valores individuais são coletados, então utilize subgrupos de tamanho um, que serão plotados em um gráfico XI. No caso de múltiplas coletas em um mesmo momento, utilize a média para definir o subgrupo e plotar os dados em um gráfico XBarra.

• Estabeleça procedimento padrão de amostragem

Tamanho e frequência de amostras devem ser mantidas. Assim como técnicas de coleta de dados não devem variar de acordo com o instrumento e operador que realiza as medições.

Portanto, quando você toma cuidado em como amostrar e agrupar os seus dados, você ganha o poder de transformar seu Gráfico de Controle em uma ferramenta informativa, eficaz e confiável para a tomada de decisão.

Veja os outros fundamentos:

Fundamento Um – Utilizar limites três sigma

Fundamento Dois – Utilizar estatística da dispersão média

Fundamento Quatro – Utilizar o conhecimento adquirido[:es]¿Qué tener en cuenta para la definición de estrategias de muestreo? ¿Cuál es la mejor manera de organizar los datos en subgrupos? Estas preguntas parecen simples, pero es fundamental conocer y comprender sus respuestas para que los análisis gráficos sean válidos. Este es el tema que vamos a cubrir en este post, que es el Tercero Fundamento de Shewhart para las Gráficas de Control.

Fundamento Tres: Muestreo y Subgrupo Racional

Muestreo Racional

 Muestreos racionales se recogen llevando en cuenta cómo y qué se mide el proceso, y cuándo y dónde se mide. Aquí hay algunas preguntas para ayudar a definir un muestreo racional.

• ¿Quién recopilará los datos?

Determine las habilidades del operador que recopilará los datos. ¿Cuánto tiempo el operador tiene? ¿El operador tiene recursos suficientes para recopilar los datos?

• ¿Lo qué va a ser medido?

Centrarse en las características clave. ¡Recuerde siempre, las mediciones son caras! Hay que centrarse en las características que son fundamentales para controlar el proceso.

• ¿Dónde se saca la muestra?

La muestra debe ser sacada en un punto del proceso que permite que los datos sean utilizados para el control de proceso.

• ¿Cuándo se saca la muestra del proceso?

Las muestras deben ser sacadas con suficiente frecuencia para reflejar los cambios en el proceso.

• ¿Por qué estamos midiendo?

Las informaciones recogidas deben posibilitar la toma de acción en los procesos. ¿Los datos serán utilizados para el control del proceso o control del producto?

• ¿Cómo se recopilarán los datos?

Se debe establecer un procedimiento estándar para la recopilación de datos. Instrumentos y operadores diferentes no deben interferir en los resultados obtenidos.

• ¿Cuántas piezas se medirán?

Las muestras deben ser aleatorias y representativas. El tamaño de muestreo debe ser suficiente para controlar el proceso, sin ser demasiado grande, causando grandes costos, pérdida de tiempo o productividad.

Subgrupo Racional

Una vez que el muestreo se recogió de una manera racional, los datos también deben agruparse racionalmente. Esta agrupación se llama subgrupo, es decir, un conjunto de individuos registrados como un punto en la gráfica. Subgrupo racional es uno donde es poco probable presentar variaciones por causas atribuibles dentro del subgrupo. Hay algunos principios para agrupar subgrupos que deben ser utilizados en la construcción de las Gráficas de Control, que son:

• Nunca agrupar diferentes cosas en un subgrupo

No mezcle informaciones de distintos procesos, distintos productos, distintos momentos…. Informaciones de fuentes diferentes deben ser evaluadas individualmente, de lo contrario, informaciones importantes pueden ser enmascaradas y conclusiones erróneas pueden ser tomadas.

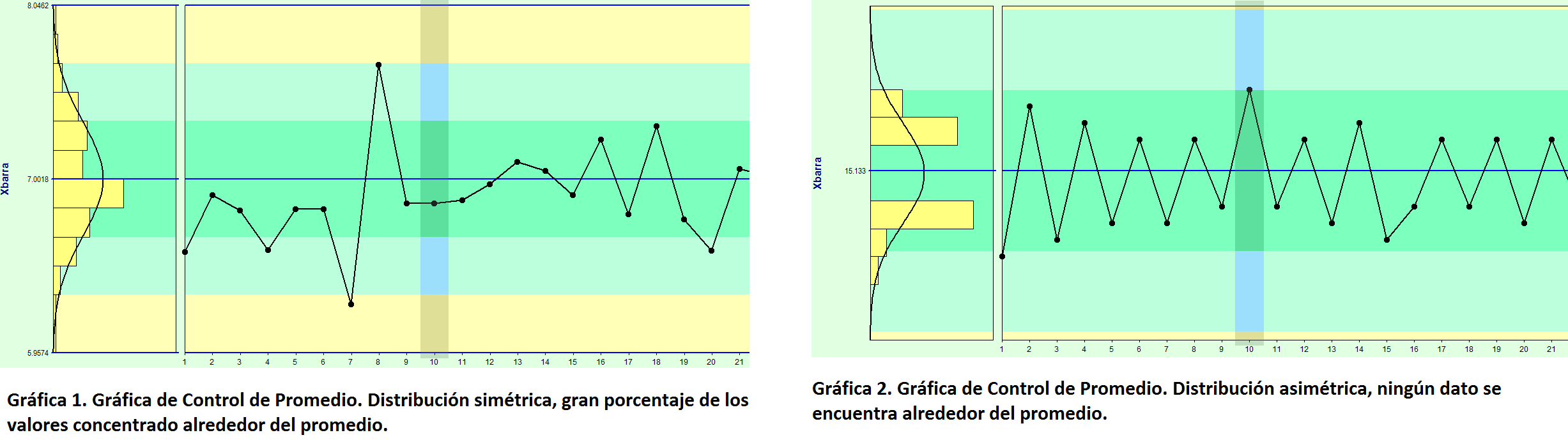
Por ejemplo, los productos de diferentes líneas de producción no deben mezclarse en un subgrupo. En la Gráfica 1, podemos ver que la distribución es simétrica, no indica una mezcla de información diferente. Ya en la Gráfica 2, se observa que la distribución de los datos se acumula lejos del promedio del proceso, esto es señal de una mezcla de información (por ejemplo, la salida de dos líneas distintas). En este caso, los datos deben ser analizados por separado, de modo que la información se trasluce la realidad de producción.

• Minimizar la variación en cada subgrupo

La variación dentro de cada subgrupo interfiere directamente en los límites de control. Al minimizar la variación dentro del subgrupo, usted estará creando una Gráfica de Control que será sensible a las señales del proceso (causas asignables – grandes variaciones), porque sólo el ruido (causas aleatorias – pequeñas variaciones) serán considerados para definir la variación del proceso.

Si solamente hay variaciones aleatorias en los subgrupos, las diferencias entre o dentro de los subgrupos serán asignados a causas asignables.

• Maximizar la oportunidad de variación entre los subgrupos

Si hay posibilidades de interferencias, asegúrese de que están en diferentes subgrupos. La gráfica de promedio analiza las diferencias entre los subgrupos. Ella utiliza la variación dentro del subgrupo para saber cuánta variación debe ser ignorada entre los subgrupos y así detectar las causas asignables.

• Realizar el promedio de cosas similares, no de cosas diferentes

El objetivo de utilizar el promedio de subgrupos es agrupar cosas donde sólo ruidos (variaciones inherentes al proceso) actúan para que sea fácil identificar cuando una señal esté actuando en el proceso.

• Utilizar la gráfica apropiada para el tipo de dato

Si se recogen valores individuales, entonces utilice subgrupos de tamaño uno, que se representan en la gráfica XI. En el caso de varias recopilaciones al mismo tiempo, utilice el promedio para definir el subgrupo y represente los datos en una gráfica XBarra.

• Establezca el procedimiento estándar de muestreo

El tamaño y la frecuencia de muestreo deben mantenerse. Así como las técnicas de recopilación de datos no deben variar de acuerdo con el instrumento y el operador que realiza las mediciones.

Por lo tanto, cuando si tiene cuidado en cómo realizar el muestreo y agrupar los datos, usted adquiere el poder de transformar su Gráfica de Control en una herramienta informativa, eficaz y confiable para la toma de decisiones.

Vea los demás fundamentos:

Fundamento Uno – Utilizar límites tres sigma

Fundamento Dos – Utilizar estadística de dispersión promedio

Fundamento Cuatro – Utilizar el conocimiento adquirido[:]