[:pb]Alguns dos questionamentos que escutamos com frequência nos treinamentos que a HarboR oferece – seja quando estamos falando especificamente de Controle Estatístico de Processos ou de como usar o InfinityQS para aplicar o CEP – é: E quanto a normalidade? Precisamos de dados normais para poder usar os Gráficos de Controle, certo?
A resposta curta e simples – e que contraria muito do que se diz por aí – é: não, não precisamos de dados normais!
A resposta longa e convincente nós veremos ao longo desse post. Vamos lá?
Porque não precisamos de dados normais
Os Limites de Controle 3sigma são suficientemente robustos para trabalhar com todos os tipos de dados, não apenas com dados normalmente distribuídos. Não é necessário ter dados normais.
A função do Gráfico de Controle é separar a variação de rotina do processo –produzida por causas aleatórias – da variação excepcional – provocada por causas atribuíveis.
O impacto da variação excepcional sobre o processo é, por definição, predominante quando comparado ao impacto das variações aleatórias. Sendo assim, os Limites de Controle precisam filtrar apenas a maior parte da variação de rotina para distinguir o que é ruído do que é sinal do processo. Por isso precisamos de Limites de Controle que cubram toda, ou quase toda variação de rotina.
Para entender como os Limites de Controle 3sigma fazem isso, podemos usar vários modelos de probabilidade para caracterizar a variação de um processo. Na figura abaixo, apresentamos seis modelos – que vão desde a distribuição uniforme até a distribuição exponencial:
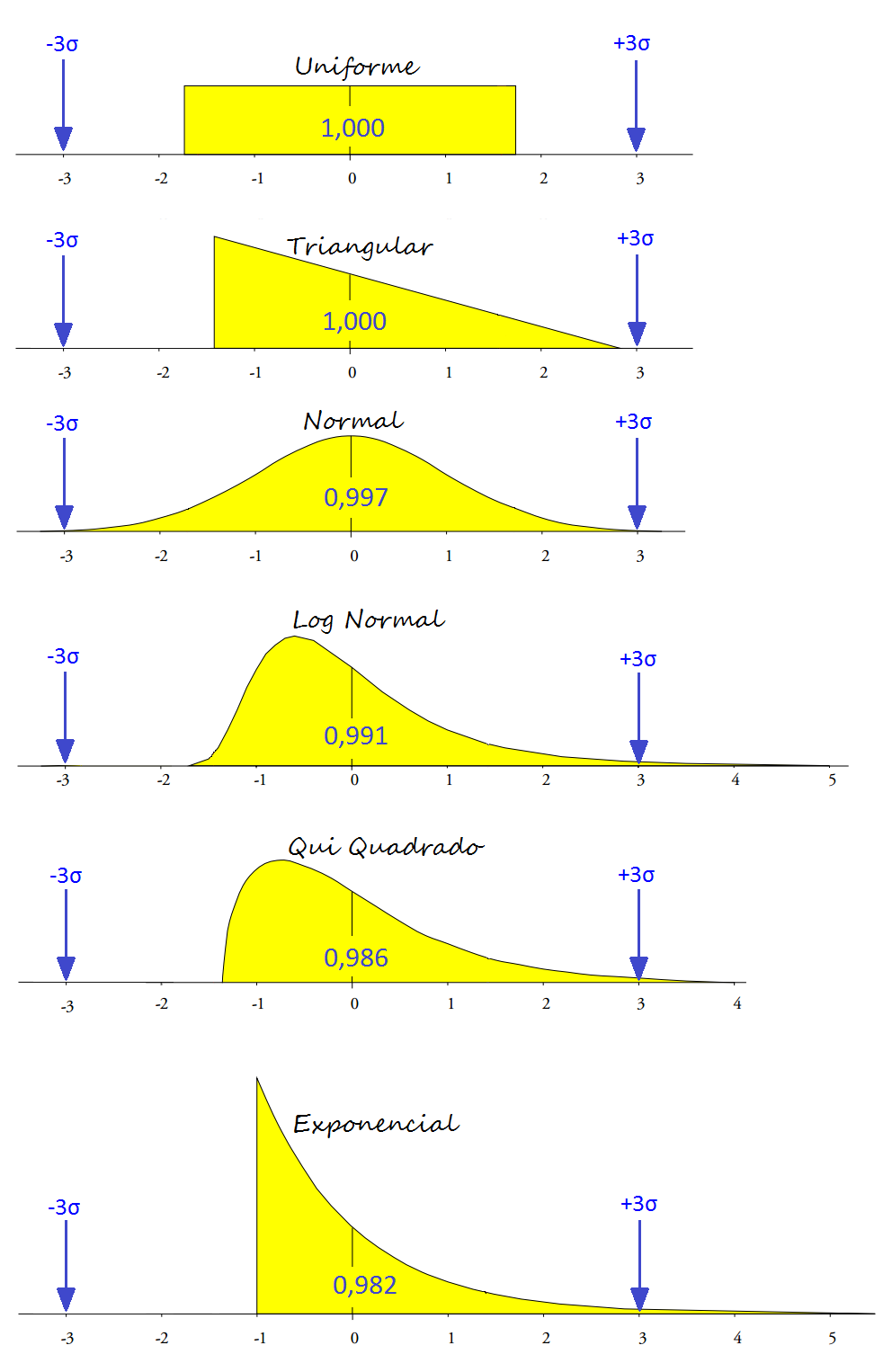 No exemplo acima, todos os modelos foram padronizados com média igual a 0 e desvio padrão igual 1. Ao observar os Limites de Controle definidos pela região de -3 a +3 sigma e a proporção da área de cada curva que está dentro desses limites, aprendemos quatro lições:
No exemplo acima, todos os modelos foram padronizados com média igual a 0 e desvio padrão igual 1. Ao observar os Limites de Controle definidos pela região de -3 a +3 sigma e a proporção da área de cada curva que está dentro desses limites, aprendemos quatro lições:
#1 – Limites de Controle são efetivos para diferente distribuições
O exemplo nos mostra que independentemente do formato da distribuição apresentada pelos processos, os Limites de Controle irão separar praticamente toda a variação de rotina da variação excepcional.
Os modelos de distribuição de dados trabalhados aqui são drasticamente diferentes. Apesar da diferença entre os modelos, os Limites de Controle cobrem de 98 a 100% dos dados.
#2 – Pontos fora dos limites representam sinais
Ao observar as diferentes distribuições estudadas, vemos que qualquer ponto que cair fora dos Limites de Controle é um sinal potencial de uma mudança de processo.
Independente da distribuição que os dados tiverem, é muito pequena a probabilidade de ter um ponto fora dos Limites de Controle e esse dado representar a variação rotineira do processo. É mais provável que qualquer ponto fora desses limites seja um sinal de uma mudança de processo.
#3 – Limites simétricos funcionam para dados assimétricos
Limites de Controle são simétricos por definição, mas funcionam com dados assimétricos. Entre os seis modelos apresentados, quatro são assimétricos.
Não importa o quão assimétricos sejam os dados, o parâmetro de desvio padrão é esticado na mesma proporção que a cauda da curva. Isso significa que o comprimento da cauda alongada determinará efetivamente a distância de três sigma em cada caso. Assim, os limites irão cobrir a maior parte da cauda alongada, não importa o quão assimétricos os dados sejam.
Ter dados assimétricos – ou não ter dados normais – não impede de trabalhar com os Limites de Controle. Porém, é necessário ter nesses casos atenção especial com as regras de alarme ativadas no Gráfico de Controle. É possível que para determinadas regras ocorram alarmes falsos, mas esse é assunto para um próximo post 😉
#4 – Não se preocupe tanto com a incerteza
Qualquer incerteza sobre aonde definimos exatamente os Limites de Controle não afetará consideravelmente a cobertura dos Limites.
Isso porque ao aproximar-se da região de -3 e +3 sigma, independente da normalidade da distribuição, as curvas são tão planas que qualquer erro que possamos cometer ao estimar os limites terão – quando tiverem – um impacto mínimo sobre o funcionamento do Gráfico de Controle.
De onde vêm essas distribuições?
Os seis modelos de probabilidade aqui apresentados são o resumo de um extenso trabalho feito por Donald J. Wheeler – autor de numerosos livros sobre Controle Estatístico de Processos publicados pela SPC Press. Tópicos relacionados a dados normais e os Gráficos de Controle são especialmente trabalhados em seu livro Normality and the Process Behavior Chart, publicado pela mesma editora.
Esses modelos resumem efetivamente o que foi encontrado pelo autor ao examinar 1143 modelos de probabilidade entre 7 famílias de modelos de uso comum. O estudo cobriu 916 modelos em forma de sino, 182 modelos em forma de J e 45 modelos em forma de U. Entre os 1143 modelos analisados, 1112 tiveram mais do que 97,5% da área da curva coberta pelos limites simétricos de 3sigma.
Derrubando o mito dos dados normais
Os Limites de Controle estimados a 3 sigma da média do processo são calculados com base na distribuição normal. Porém, como vimos, isso não significa que os dados precisam ser normalmente distribuídos.
Limites de Controle calculados a três sigma da média são suficientemente robustos para trabalhar com a grande maioria de distribuições de dados. Eles são efetivos para trabalhar com dados descontínuos ou assimétricos, ou seja, quando não temos dados normais.
Por isso:
- Não é necessário nenhum tipo de tratamento de dados antes de colocá-los em um Gráfico de Controle;
- Não é preciso definir uma distribuição de referência antes de estimar os Limites de Controle;
- Também não é necessário transformar os dados antes de colocá-los em um Gráfico de Controle.
Confie na robustez do Gráfico de Controle e lembre-se que quanto mais simples, melhor!
Além do “mito da normalidade”, selecionamos outros 8 erros a evitar na implementação do CEP, continue a leitura!
Se você se interessou pelo conteúdo, conheça mais sobre o Treinamento de CEP que podemos ministrar na sua empresa! [:es]Algunos de los cuestionamientos que escuchamos con frecuencia en los entrenamientos que HarboR ofrece – sea cuando estamos hablando específicamente de Control Estadístico de Procesos o de cómo usar InfinityQS para aplicar el SPC – es: ¿Y en cuanto a la normalidad? Necesitamos datos normales para poder usar las Gráficas de Control, ¿verdad?
La respuesta corta y simple – y que contraría mucho de lo que se dice por ahí – es: ¡no, no necesitamos datos normales!
La respuesta larga y convincente veremos a lo largo de este post. ¿Vamos allá?
Porque no necesitamos datos normales
Los Límites de Control 3sigma son lo suficientemente robustos para trabajar con todos los tipos de datos, no sólo con datos normalmente distribuidos. No es necesario tener datos normales.
La función de la Gráfica de Control es separar la variación de rutina del proceso -producida por causas aleatorias – de la variación excepcional – provocada por causas especiales.
El impacto de la variación especial sobre el proceso es, por definición, predominante en comparación con el impacto de las variaciones aleatorias. Siendo así, los Límites de Control deben filtrar sólo la mayor parte de la variación de rutina para distinguir lo que es ruido de lo que es señal del proceso. Por eso necesitamos Límites de Control que cubran toda, o casi toda variación de rutina.
Para entender cómo los Límites de Control 3sigma lo hacen, podemos usar varios modelos de probabilidad para caracterizar la variación de un proceso. En la figura siguiente, presentamos seis modelos – que van desde la distribución uniforme hasta la distribución exponencial:
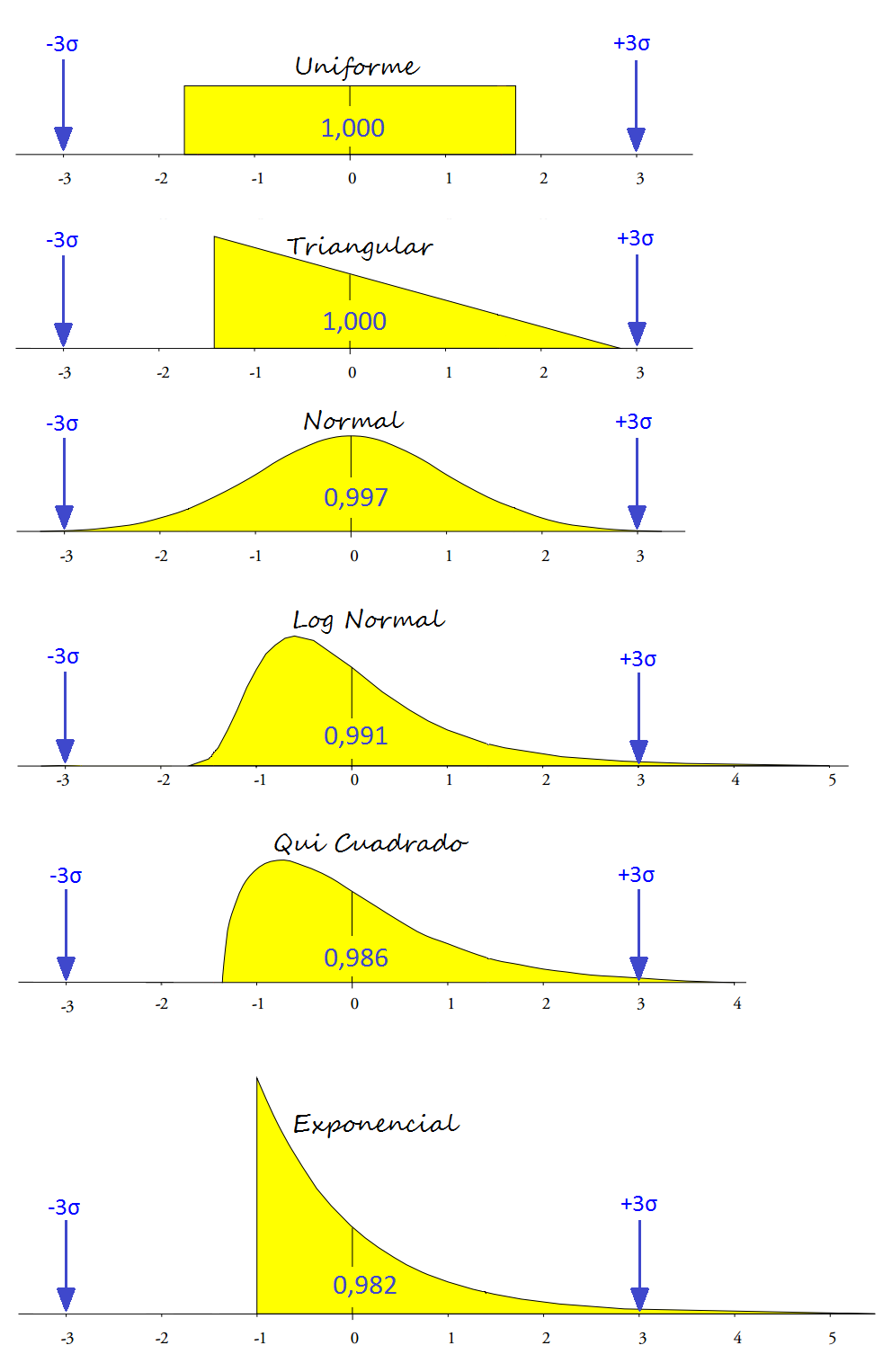 En el ejemplo anterior, todos los modelos fueron estandarizados con promedio igual a 0 y desviación estándar igual 1. Al observar los Límites de Control definidos por la región de -3 a +3 sigma y la proporción del área de cada curva que está dentro de esos límites, aprendemos cuatro lecciones:
En el ejemplo anterior, todos los modelos fueron estandarizados con promedio igual a 0 y desviación estándar igual 1. Al observar los Límites de Control definidos por la región de -3 a +3 sigma y la proporción del área de cada curva que está dentro de esos límites, aprendemos cuatro lecciones:
#1 – Límites de control son efectivos para diferentes distribuciones
El ejemplo nos muestra que independientemente del formato de la distribución presentada por los procesos, los Límites de Control separarán prácticamente toda la variación de rutina de la variación excepcional.
Los modelos de distribución de datos trabajados aquí son drásticamente diferentes. A pesar de la diferencia entre los modelos, los Límites de Control cubren del 98 al 100% de los datos.
#2 – Puntos fuera de los límites representan señales
Al observar las diferentes distribuciones estudiadas, vemos que cualquier punto que caiga fuera de los Límites de Control es una señal potencial de un cambio de proceso.
Independiente de la distribución que los datos tengan, es muy pequeña la probabilidad de tener un punto fuera de los Límites de Control y ese dado representar la variación rutinaria del proceso. Es más probable que cualquier punto fuera de esos límites sea una señal de un cambio de proceso.
#3 – Límites simétricos funcionan para datos asimétricos
Los Límites de Control son simétricos por definición, pero funcionan con datos asimétricos. Entre los seis modelos presentados, cuatro son asimétricos.
No importa cuán asimétricos sean los datos, el parámetro de desviación estándar se estira en la misma proporción que la cola de la curva. Esto significa que la longitud de la cola alargada determinará efectivamente la distancia de tres sigmas en cada caso. Así, los límites cubrirán la mayor parte de la cola alargada, no importa cuán asimétricos sean los datos.
Tener datos asimétricos – o no tener datos normales – no impide de trabajar con los Límites de Control. Sin embargo, es necesario tener en estos casos atención especial con las reglas de alarma activadas en la Gráfica de Control. Es posible que para ciertas reglas se produzcan alarmas falsas, pero este es asunto para un próximo post 😉
# 4 – No se preocupe tanto por la incertidumbre
Cualquier incertidumbre sobre dónde definimos exactamente los Límites de Control no afectará considerablemente la cobertura de los límites.
Esto es porque al acercarse a la región de -3 y +3 sigmas, independientemente de la normalidad de la distribución, las curvas son tan planas que cualquier error que podamos cometer al estimar los límites tendrá – cuando tenga – un impacto mínimo sobre el funcionamiento de la Gráfica de Control.
¿De dónde vienen esas distribuciones?
Los seis modelos de probabilidad aquí presentados son el resumen de un extenso trabajo hecho por Donald J. Wheeler – autor de numerosos libros sobre Control Estadístico de Procesos publicados por la SPC Press. Los temas relacionados con los datos normales y las Gráficas de Control están especialmente trabajados en su libro Normality and the Process Behavior Chart, publicado por la misma editora.
Estos modelos resumen efectivamente lo que fue encontrado por el autor al examinar 1143 modelos de probabilidad entre 7 familias de modelos de uso común. El estudio cubrió 916 modelos en forma de campana, 182 modelos en forma de J y 45 modelos en forma de U. Entre los 1143 modelos analizados, 1112 tuvieron más del 97,5% del área de la curva cubierta por los límites simétricos de 3sigma.
Acabando con el mito de los datos normales
Los Límites de Control estimados a 3 sigmas del promedio del proceso se calculan sobre la base de la distribución normal. Sin embargo, como hemos visto, esto no significa que los datos deben ser normalmente distribuidos.
Los Límites de Control calculados a tres sigmas del promedio son lo suficientemente robustos para trabajar con la gran mayoría de las distribuciones de datos. Ellos son efectivos para trabajar con datos discontinuos o asimétricos, o sea, cuando no tenemos datos normales.
Por eso:
- No es necesario ningún tipo de tratamiento de datos antes de colocarlos en una Gráfica de Control;
- No es necesario definir una distribución de referencia antes de estimar los Límites de Control;
- También no es necesario transformar los datos antes de colocarlos en una Gráfica de control.
¡Confía en la robustez de la Gráfica de Control y recuerde que cuanto más simple, mejor!
Además del “mito de la normalidad”, seleccionamos otros 8 errores a evitar en la implementación del SPC, ¡continúe la lectura!
Si te interesaste por el contenido, conozca más sobre el Entrenamiento de SPC que podemos ministrar en tu empresa.[:]

![You are currently viewing [:pb]Normalidade e CEP – Precisamos de dados normais?[:es]Normalidad y SPC – ¿Necesitamos datos normales?[:]](https://novosite.harbor.com.br/wp-content/uploads/2018/01/imagem-destaque-blog-1-e1516303903210.png)
![Read more about the article [:pb]Variação é sinônimo de falta de qualidade?[:es]La variación es sinónimo de falta de calidad?[:]](https://novosite.harbor.com.br/wp-content/uploads/2017/06/variacao_qualidade-300x200.png)
![Read more about the article [:pb]Porque devo utilizar Checklist na minha empresa?[:es]¿Por qué debo utilizar Checklist en mi empresa?[:]](https://novosite.harbor.com.br/wp-content/uploads/2019/01/checklist-1919328_960_720-300x221.png)
![Read more about the article [:pb]Folha de verificação [7 Ferramentas da Qualidade][:]](https://novosite.harbor.com.br/wp-content/uploads/2016/08/As-7-ferramentas-da-qualidade-07-300x300.png)
Olá. Fiz um comentário há alguns dias mas acho que ele não entrou. Seu texto está bem escrito, parabéns.
Mas com relação ao ponto #4 tenho uma observação: Muitos estudos mostram que usar os limites 3-sigma com limites estimados, deteriora o desenho dos gráficos de controle (a não ser que o número de amostras para estimar os limites seja muito grande, como 3000 mil amostras, por exemplo). Quando digo “deteriorar o desempenho” quero dizer que o a probabilidade de ocorrência de um alarme falso fica muito alta ou que o número médio de amostras até um alarme falso é diferente daquele quando usa-se limites de controle não estimados. Eu tenho alguns estudos publicados sobre esse tema. Se quiser, posso deixar o link de alguns estudos com mais detalhes.
Att.,
Felipe
Olá Felipe, desculpe a demora na resposta. Infelizmente não consegui acesso ao texto completo dos artigos que você indicou, então não consigo entrar em detalhes da sua análise. O post defende que os limites de controle em 3-sigma são robustos principalmente em encontrar sinais, ou seja, alterações de média ou variância do processo, mesmo quando as curvas não são normais. Em alguns casos há um risco maior de alarmes falsos, especialmente se muitas regras de alarme forem usadas (o post alerta sobre isso). Detectar pequenas variações na média ou na variância pode ser difícil com as cartas tradicionais, e o ARL (tempo até a detecção da mudança) pode realmente ficar muito grande. Mas na grande maioria dos casos, mesmo que os valores medidos na saída do processo não sigam uma distribuição normal, os limites de 3-sigma simétricos são no mínimo um bom começo para iniciar o acompanhamento da estabilidade do processo. Alguns casos especiais realmente precisarão de definição mais criteriosa, mas podemos considerar que essas são raras exceções à regra geral.
Texto bem escrito. Infelizmente, mesmo para dados normais, os famosos “limites 3-Sigmas”, não são confiáveis.
Para mais informação ver meus artigos em:
https://onlinelibrary.wiley.com/doi/abs/10.1111/poms.12985
e
https://www.tandfonline.com/doi/abs/10.1080/00224065.2019.1571345?journalCode=ujqt20
Att.,
Felipe Jardim
Bom.. discordo do texto parcialmente… tenho vários casos reais nos quais não transformar os dados normais, e plotá-los sem antes normalizá-los, (seja pela transformação de Johnson ou Box Cox) existiram até 4 causas especiais antes não visualizadas em uma amostra individual de 100 motores de secador de cabelo….
O que é defendido no post é o que o Wheeler demonstrou no seu livro – para quase todas as distribuições que ele analisou, pelo menos 97,5% dos dados que seguem essa distribuição vão cair dentro dos limites de controle definidos como média mais ou menos três desvios padrão.
É importante lembrar que no caso da distribuição normal, 99,73% dos valores caem entre esses mesmos limites.
Portanto a probabilidade de se ter alarmes falsos (um ponto fora dos limites de controle mesmo com o processo estável) é maior se usamos os limites de três desvios padrão para dados não normais. Isso é ainda mais verdadeiro no caso de gráficos com valores individuais, como o que você citou (pois a estimativa de desvio padrão calculado pela amplitude móvel também está sujeita a um erro maior). Normalizando os dados, essa probabilidade de alarmes falsos cai.
Fazer a normalização é um processo sujeito a erros de parametrização, e difícil de fazer sem um software. Mas o principal problema é que ele tira do usuário do CEP a conexão direta com a realidade – por exemplo, ele mede um valor de rugosidade que é 29,1 no instrumento, mas vê no gráfico o valor normalizado de 387,23…
O que o post defende (assim como o Wheeler) é que fazer controle estatístico utilizando os limites clássicos de controle mesmo sem ter uma distribuição normal vai dar resultados positivos. Para quem está usando um software como o InfinityQS, optar pela carta de IX-s (valores individuais com estimativa do desvio padrão da população pelo desvio padrão dos valores amostrados) vai também dar resultados melhores.
Não conhecia a abordagem do Wheeler e seu resumo foi excelente Bruna.
Essa linha da robustez dos limites de controle podem ser considerada para as análises de performance de processo para dados não normais? Ou seja, Posso calcular Cp, Pp, Cpk e Ppk para dados não normais sem transformá-los?
Pode-se calcular os coeficientes Cp, Pp, Cpk, Ppk, porém a analise de performance deve ser considerada somente para dados que estejam normalizados, isto é, dados que após serem transformados sejam considerados normais. Só assim para poder analisar os coeficientes calculados.
Muito boa a abordagem
Usei por 3vanis o sistema infinito distribuido pela Harbor! É simplesmente fantástico.
Obrigada pelo comentário, Wilker.
É uma satisfação saber a sua opinião sobre o software InfinityQS!
Lo ideal y lo real generalmente están divorciados. En mi experiencia he trabajado la mayoría de las veces con datos, en principio, no normales. Primeramente debe estarse seguro que la falta de normalidad no sea debida a outliers o a un conunto de datos generado por una condición anormal, poco frecuente y no representativa del proceso. Si es así, se deben eliminar y volver a testear normalidad. Si aún así no son normales, podemos transformarlos y trabajar con la transformación, o ver que modelo de distribución ajusta los datos (lognormal, uniforme, weibull, valor extremo más chico/más grande, etc.) y trabajar con ese modelo, o bien si no tenemos las herramientas o el tiempo para hacer lo anterior, asumir el error de trabajarlos como si fueran normales (no siempre es posible, si fabrico toneles quizás sí, si fabrico un fármaco con impacto directo en la salud de las personas, no puedo permitirme ese error).
Gracias por su comentario, Rodolfo!
La idea que defendemos aquí es que incluso cuando los datos no son normales, no necesitaS transformarlos para trabajar con límites de control, ya que los límites de control son robustos para manejar datos no normales.