[:pb]Vamos começar este post com um desafio relacionado aos Limites de Controle: O que você acha que está acontecendo com o processo monitorado pelo Gráfico de Controle abaixo?

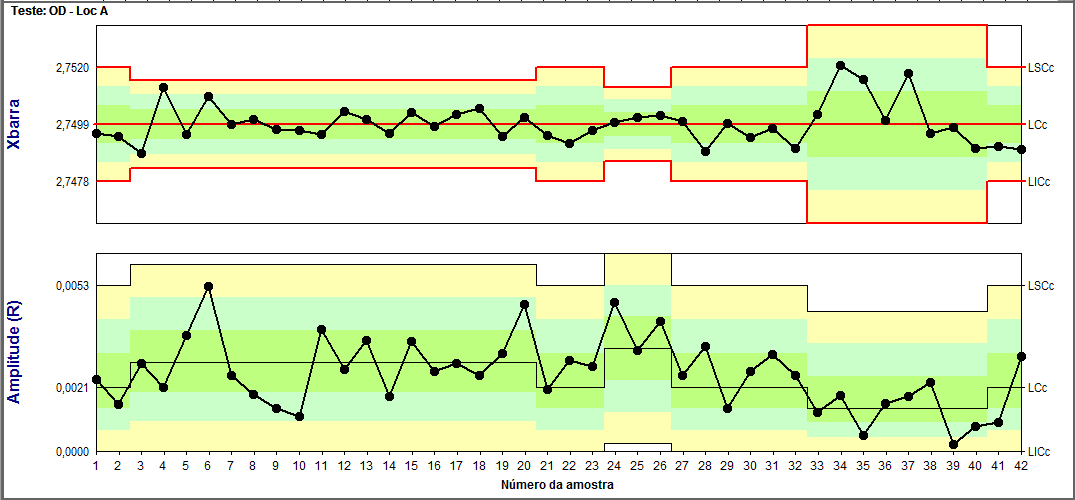
Uma possível interpretação poderia ser: “o processo sofreu ações que fizeram com que a variabilidade oscilasse, o que pode ser percebido pelos degraus nos Limites de Controle.”

Mas será que é isso mesmo?

Plano de Inspeção

Para responder ao desafio proposto no início do post, faremos algumas considerações relacionadas a planos de inspeção, pois você sabia que a maneira de executá-los interfere diretamente nos cálculos dos Limites de Controle?

Neste post não entraremos no mérito sobre quais frequências e tamanhos de amostras utilizar para definir os planos de inspeção (clique aqui e confira o post que discute muito bem isso), mas faremos uso do seguinte exemplo:

Pergunta: Se no plano de inspeção é definido que deve-se inspecionar 8 amostras por turno, em quais situações abaixo o plano de amostragem seria cumprido?

• (a) Coletar todas as amostras na primeira hora do turno
• (b) Coletar todas as amostras na  última hora do turno
• (c) Coletar 1 amostra a cada hora
• (d) Coletar 2 amostras a cada 2 horas
• (e) Coletar 5 amostras na primeira hora e 3 amostras no final do turno

Resposta: Em todos! Independente da amostragem utilizada acima, ao final do turno teremos o registro de 8 amostras.

Mas o Controle Estatístico de Processo vai muito além do que atender a uma quantidade exigida de medições. (Confira no e-book CEP – o guia definitivo os conceitos e aplicações deste excelente método).  

CEP e Plano de Inspeção

O terceiro fundamento de Shewhart apresenta as boas práticas na definição dos subgrupos. Dentre elas, temos que o tamanho da amostra também deve ser considerado no momento de definir os planos de amostragem.

Com um tamanho de amostra fixo, as estatísticas descritivas do processo tornam-se mais simples para a avaliação e interpretação por aqueles pre precisam atuar no processo se o Gráfico indicar a possível presença de causas especiais.

E o que isso tem a ver com os degraus exibidos no Gráfico de Controle no início deste post?

É que o comportamento em degraus dos Limites de Controle, neste caso, não está relacionado com mudanças no processo, e sim com o tamanho da amostra!

Relação entre Limites de Controle e Tamanho da Amostra

Para não restar dúvidas, olharemos um pouco mais a fundo a fórmula dos Limites de Controle, sabendo que:

Limites de Controle são calculados a partir da distância de 3 desvios padrão da média do processo.

Mas lembre-se que o desvio padrão da frase acima é o desvio padrão para a média dos subgrupos e não o desvio padrão de curto prazo nem o global (clique aqui e veja a diferença entre eles).

Encontra-se também na literatura o termo “erro padrão” que também se refere ao “desvio padrão estimado para a média”, que nada mais é do que o desvio padrão de curto prazo dividido pela raiz do tamanho da amostra (n).

Voltando para a definição de Limites de Controle, temos então:

Para simplificação de cálculos (lembra que essas fórmulas foram desenvolvidas por volta de 1940?), criou-se uma tabela de A₂ para os diferentes tamanhos de amostras, onde:

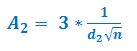
OBS: aqui temos a constante d₂, mas a origem desta fica para um próximo post 🙂

Substituíndo A₂ ali em cima, obtemos a famosa fórmula dos Limites de Controle:

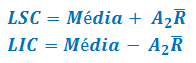
Sendo assim, quanto maior o tamanho da amostra, menor o valor de A₂ e consequentemente os Limites de Controle ficam mais apertados.

De volta ao desafio

Abaixo adicionamos no cabeçalho o tamanho da amostra utilizado no cálculo da média de cada ponto. O pontilhado vermelho destaca onde o tamanho da amostra é igual a 5, mas no Gráfico temos também pontos com tamanho 3, 7 e 1.

Com esta informação podemos agora perceber que o que faz o limite de controle variar é o tamanho da amostra.

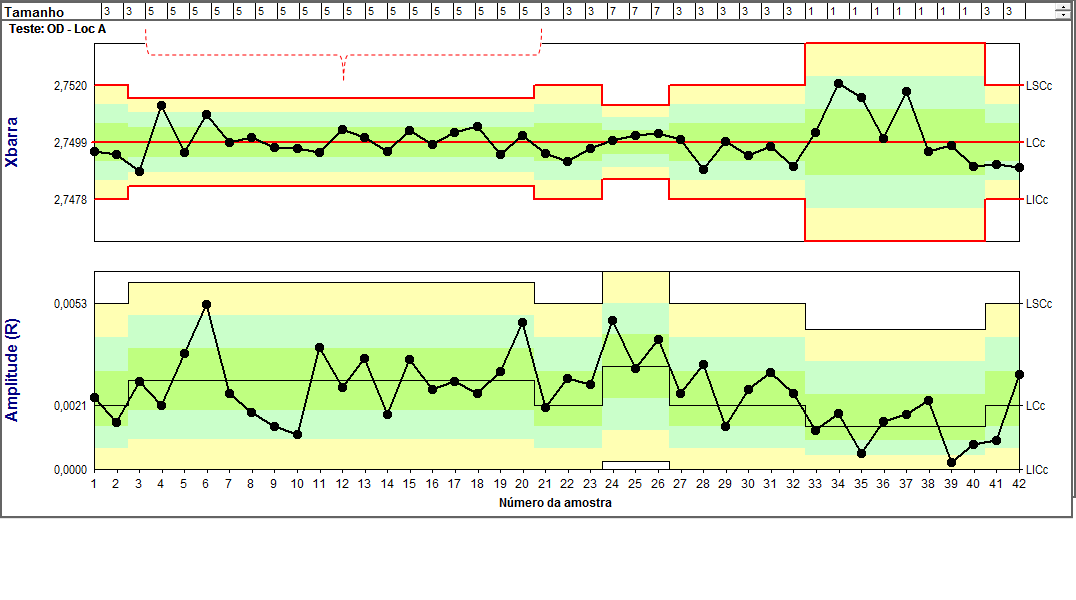
É intuitivo que quanto menor a amostra medida, menos informação temos sobre o processo, e portanto maior a probabilidade de cometermos erros de avaliação. Por isso os Limites de Controle do Gráfico das Médias ficam mais abrangentes.

Conclusão

A pergunta no início deste post ficou parecendo uma pegadinha né? Na verdade ela é, pois não existia informação suficiente para entender de fato o que estava ocorrendo.

Portanto, lembre-se:

• O Limite de Controle dos Gráficos de CEP considera o tamanho da amostra, ou seja, quantos itens são inspecionados a cada amostragem, a fim de calcular a média e variação.
• Por isso é importante definir uma estratégia de amostragem e seguir com ela de forma consistente.
• Claro que pode-se optar por alterar o tamanho da amostra (medir custa dinheiro!), mas é algo que deve-se aplicar com consistência, ou seja, não ficar alterando o tamanho de amostra a cada semana…
• É preciso adotar um método e segui-lo a fim proporcionar um monitoramento do processo mais simples para quem precisa de fato tomar alguma ação sobre o processo caso ocorra alguma causa especial (fica complicado interpretar um Gráfico cheio de degraus não é mesmo?).

E você? Já havia visto um Gráfico de Controle cheio de degraus? No seu processo produtivo, costuma variar o tamanho da amostra?

Compartilhe conosco nos comentários.[:es]Vamos a empezar este post con un desafío relacionado con los Límites de Control: ¿Qué crees que está sucediendo con el proceso monitoreado por la Gráfica de Control a continuación?

Una posible interpretación podría ser: “el proceso sufrió acciones que hicieron que la variabilidad oscila, lo que puede ser percibido por los escalones en los Límites de Control.”

Pero, ¿es realmente eso?

Plan de Inspección

Para responder al desafío propuesto al inicio del post, haremos algunas consideraciones relacionadas a los planes de inspección, pues ¿usted sabía que la manera de ejecutarlos interfiere directamente en los cálculos de los Límites de Control?

En este post no entraremos en el mérito sobre qué frecuencias y tamaños de muestras utilizar para definir los planes de inspección (haga clic aquí y vea el post que discute muy bien eso (disponible sólo en Portugués), pero haremos uso del siguiente ejemplo:

Pregunta: ¿Si se define en el plan de inspección que se deben inspeccionar 8 muestras por turno, en qué situaciones abajo el plan de muestre se cumplirá?

• (a) Recoger todas las muestras a la primera hora del turno
• (b) Recoger todas las muestras a la última hora del turno
• (c) Recoger 1 muestra cada hora
• (d) Recoger 2 muestras cada 2 horas
• (e) Recoger 5 muestras a la primera hora y 3 muestras al final del turno

Respuesta: ¡En todos! Independiente del muestreo utilizado arriba, al final del turno tendremos el registro de 8 muestras.

Pero el Control Estadístico de Proceso (SPC) va mucho más allá de atender a una cantidad requerida de mediciones. (Ver en el e-book SPC – la guía definitiva los conceptos y aplicaciones de este excelente método (disponible sólo en Portugués)).

SPC y Plan de Inspección

El tercer fundamento de Shewhart presenta las buenas prácticas en la definición de los subgrupos. Entre ellas, tenemos que el tamaño de la muestra también debe ser considerado en el momento de definir los planes de muestreo.

Con un tamaño de muestra fijo, las estadísticas descriptivas del proceso se vuelven más simples para la evaluación e interpretación por aquellos que necesitan actuar en el proceso si la Gráfica indicar la posible presencia de causas especiales.

¿Y qué tiene que ver con los escalones que aparecen en la Gráfica de Control al principio de este post?

Es que el comportamiento en escalones de los Límites de Control, en este caso, no está relacionado con cambios en el proceso, sino ¡con el tamaño de la muestra!

Relación entre Límites de Control y Tamaño de Muestra

Para no quedar dudas, miraremos un poco más a fondo la fórmula de los Límites de Control, que por definición, sabemos que:

Los Límites de Control se calculan a partir de la distancia de 3 desviaciones estándar del promedio del proceso.

Pero recuerde que la desviación estándar de la frase anterior es la desviación estándar para el promedio de los subgrupos y no la desviación estándar de corto plazo ni el global (haga clic aquí y vea la diferencia entre ellos).

Se encuentra también en la literatura el término “error estándar” que también se refiere a la “desviación estándar estimada para el promedio”, que no es más que la desviación estándar de corto plazo dividida por la raíz del tamaño de la muestra (n).

Volviendo a la definición de Límites de Control, tenemos entonces:

Para simplificar los cálculos (¿recuerda que estas fórmulas se desarrollaron alrededor de 1940?), se creó una tabla de A₂ para los diferentes tamaños de muestra, donde:

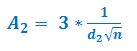
OBS: aquí tenemos la constante d₂, pero el origen de este se queda para un próximo post 🙂

Sustituyendo A₂ allí arriba, obtenemos la famosa fórmula de los Límites de Control:

Siendo así, cuanto mayor sea el tamaño de la muestra, menor el valor de A₂ y consecuentemente los Límites de Control quedan más apretados.

De vuelta al desafío

A continuación añadimos en el encabezado el tamaño de la muestra utilizado en el cálculo del promedio de cada punto. El punteado rojo destaca donde el tamaño de la muestra es igual a 5, pero en la Gráfica tenemos también puntos con tamaño 3, 7 y 1.

Con esta información podemos ahora percibir que lo que hace que el Límite de Control varía es el tamaño de la muestra.

Es intuitivo que cuanto menor sea la muestra medida, menos información tenemos sobre el proceso, y por lo tanto mayor es la probabilidad de cometer errores de evaluación. Por lo que los Límites de Control de la Gráfica del promedio son más amplios.

Conclusión

La pregunta al principio de este post se parece a una trampa ¿no es así? En realidad lo es, pues no tenía información suficiente para entender de hecho lo que estaba ocurriendo.

Por lo tanto, recuerde:

• El Límite de Control de las Gráficas de SPC considera el tamaño de la muestra, es decir, cuántos elementos son inspeccionados a cada muestra, a fin de calcular el promedio y la variación.
• Por eso es importante definir una estrategia de muestreo y seguir con ella de forma consistente.
• Por supuesto, se puede optar por cambiar el tamaño de la muestra (medir cuesta dinero!), pero es algo que se debe aplicar con consistencia, es decir, no cambiar el tamaño de muestra cada semana …
• Es necesario adoptar un método y seguirlo para proporcionar un monitoreo del proceso más simple para quien necesita de hecho tomar alguna acción sobre el proceso en caso de ocurrir alguna causa especial (es complicado interpretar un gráfico lleno de peldaños no es así?).

¿Y usted? Ya había visto una Gráfica de Control llena de escalones? En su proceso productivo, ¿suele variar el tamaño de la muestra?

Comparta con nosotros en los comentarios.[:]