• Zona C = Distância entre Média ± 1σ_x
• Zona B = Distância entre ±1σ_x e ± 2σ_x 
• Zona A = Distância entre ±2σ_x e ± 3σ_x 

Se os pontos estão próximos da linha central e com pouquíssima variação, o processo não estaria ótimo?

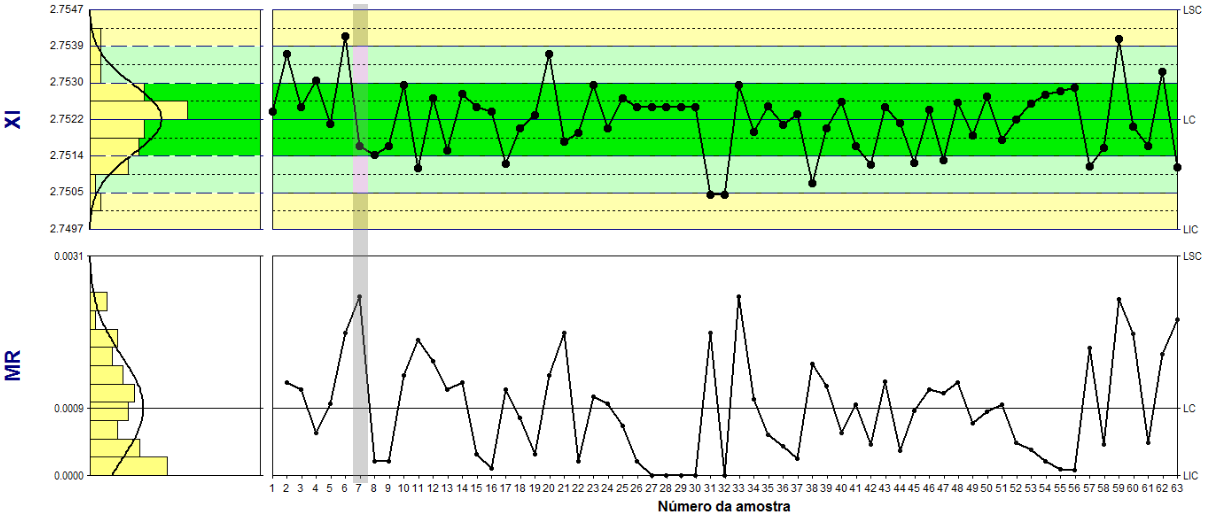
• LC (média do processo) =  2.7522
• LSC = 2.7547
• LIC = 2.7497
• Amplitude média (LC do gráfico MR) = 0.0009
• O processo esta sob Controle Estatístico pois não foi observado nenhum valor fora dos limites de controle e nenhum outra regra foi alcançada.

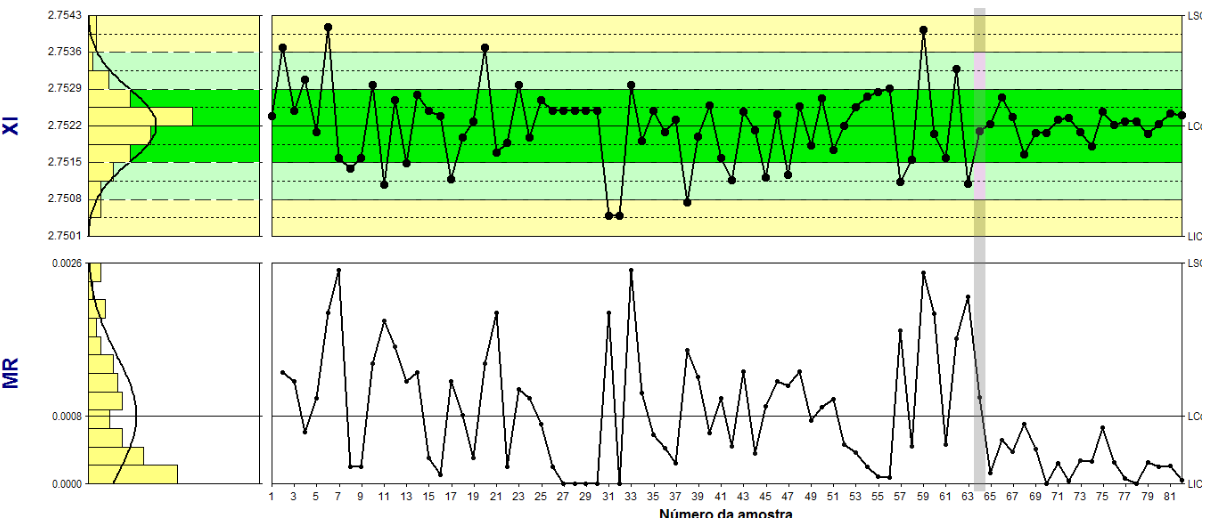E agora, o processo ainda pode ser considerado sob Controle Estatístico?

No CEP, consideramos que o processo está sob controle estatístico quando a variação observada é fruto apenas de causas aleatórias, sendo o Gráfico de Controle uma ferramenta eficaz para nos auxiliar neste julgamento.

A cada ponto que medimos e plotamos, estamos na verdade perguntando para o Gráfico o seguinte:

“Posso considerar que o meu processo está sob controle, ou seja, continua produzindo com a mesma média e desvio padrão conhecidos?”

Quando os pontos variam dentro dos limites de controle aleatoriamente conforme as probabilidades de cada zona, o Gráfico está respondendo: “SIM, pode considerar o seu processo sob controle“.

• Neste exemplo, a regra de 15 pontos consecutivos variando na zona C, NÃO é para dizer:

“Ei! Seu processo não está bom, pois ele esta variando pouco” (não faz sentido né?). 

• Em vez disso, ela quer nos dizer:  

“Ei! Seu processo está ótimo!! A variação diminuiu muito! Algo aconteceu que manteve a média conhecida, porém diminuiu drasticamente a variabilidade. Então pare o que está fazendo e vá investigar qual foi a causa especial que atuou sobre o processo para que possamos mantê-la“.

GRÁFICO 3:

Para visualizar melhor os novos limites, no Gráfico 4 estão sendo exibidos apenas os pontos após a causa especial.

GRÁFICO 4:

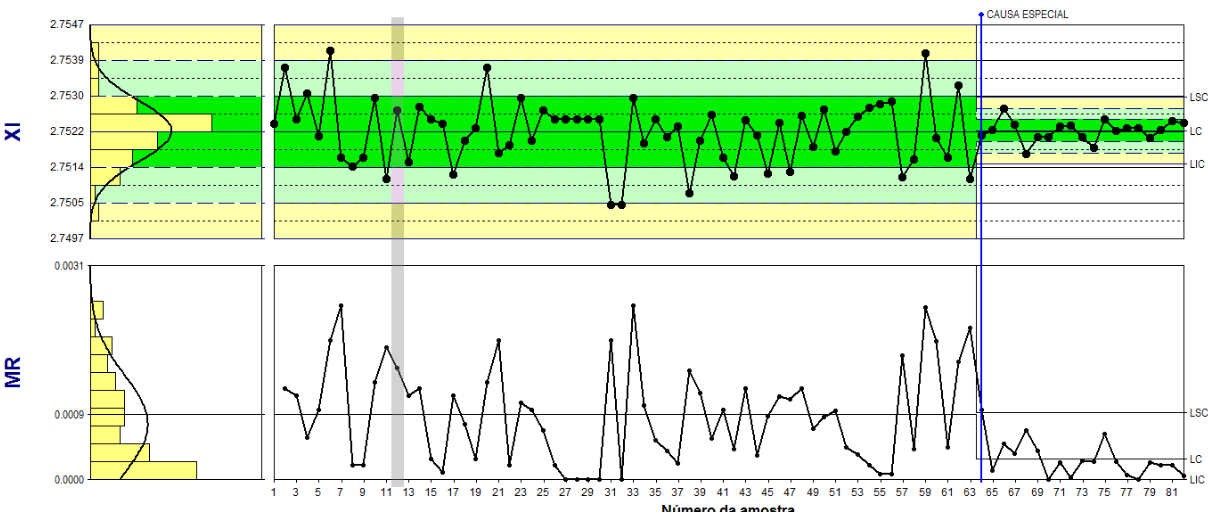
Perceba como alteraram algumas estatísticas:

• LC (média do processo) =  era 2.7522 e agora é 2.7522 (se manteve)
• LSC = era  2.7547 e agora é 2.7530
• LIC = 2.7497 e agora é 2.7515
• Amplitude média (LC do gráfico MR) = era 0.0009 e agora é 0.0003

 

CONCLUINDO, podemos dizer que a regra de 15 pontos consecutivos na zona C é muito valiosa*, já que pode identificar que alguma melhoria ocorreu no processo. 

*Neste exemplo, usamos a abordagem de que a causa especial foi uma indicação de algo positivo, porém, nem sempre é assim. Pode-se, por exemplo, ter um equipamento de medição descalibrado ocasionando medições com pouca precisão, o que é algo negativo, mas que precisa também ser identificado o mais rápido possível. 

 

• LC (promedio del proceso) =  2.7522
• LSC = 2.7547
• LIC = 2.7497
• Rango promedio (LC de la gráfica MR) = 0.0009
• El proceso está bajo control estadístico pues no se observó ningún valor fuera de los límites de control y no se alcanzó ninguna otra regla.

Continuando los muestreos y trazando otros 19 puntos en la Gráfica 1, obtenemos la Gráfica 2:

GRÁFICA 2:

¿Y ahora, el proceso todavía puede ser considerado bajo Control Estadístico?
Bueno, lo que nadie puede negar es que el proceso ha mejorado, pues los nuevos puntos están cayendo más cerca de la línea central.
Pero volviendo la pregunta, ¿el proceso aún está bajo control estadístico?

En el SPC, consideramos que el proceso está bajo control estadístico cuando la variación observada es fruto sólo de causas aleatorias, siendo la Gráfica de Control una herramienta eficaz para ayudarnos en este juicio.
En cada punto que medimos y trazamos, estamos en realidad preguntando a la Gráfica lo siguiente: “¿Puedo considerar que mi proceso está bajo control, o sea, continúa produciendo con el mismo promedio y desviación estándar conocidos?“

Cuando los puntos varían dentro de los límites de control de forma aleatoria conforme a las probabilidades de cada zona, la Gráfica está respondiendo: “SI, puede considerar su proceso bajo control“.

Ahora observe de nuevo la Gráfica 2 y responda lo siguiente: ¿El proceso continúa con el mismo promedio y desviación estándar? El promedio se mantuvo, pero la desviación estándar disminuyó ¿no es verdad?

Suponiendo que una alarma en la Gráfica de Control es una fuerte indicación de que una causa especial está actuando sobre el proceso, tenemos como trata de investigar el proceso para eliminar la causa a fin de “traer” el proceso nuevamente a la condición bajo control.

Pero en el caso de la Gráfica 2, la alarma es una indicación de algo POSITIVO, pues según el histórico del proceso, se esperaba que los puntos fueran a variar de forma aleatoria entre los límites de controles, ¡pero ellos están variando muy poco! Por lo tanto, ocurrió alguna causa que hizo que la variación disminuyera mucho.

• En este ejemplo, la regla de 15 puntos consecutivos en la zona C, NO es para decir:

“¡Vaya! Su proceso no está bien, pues él esta variando poco” (¿no tiene sentido verdad?).

• En cambio, quiere decirnos:

“¡Vaya! Su proceso está muy bien! ¡La variación disminuyó mucho! Algo ocurrió que mantuvo el promedio conocido, pero disminuyó drásticamente la variabilidad. Entonces detenga lo que está haciendo y vaya a investigar cuál fue la causa especial que actuó sobre el proceso para que podamos mantenerla.”

Si es posible hacer que la causa especial que disminuyó la variabilidad sea incorporada al proceso, entonces el proceso ya no será el mismo cuando los límites de control fueron definidos. Es decir, esta regla también es un indicativo de que los límites de control pueden ser re-calculados.

En la Gráfico 3 tenemos los mismos datos de la Gráfico 2, pero re-calculamos los límites de control sólo con los puntos después de la causa especial.

GRÁFICA 3:

Para ver mejor los nuevos límites, en la Gráfico 4 sólo se muestran los puntos después de la causa especial.

GRÁFICA 4:

Percibe cómo han cambiado algunas estadísticas:
LC (promedio del proceso) = era 2.7522 y ahora es 2.7522 (se mantuvo)
LSC = era 2.7547 y ahora es 2.7530
LIC = 2.7497 y ahora es 2.7515
Amplitud media (LC del gráfico MR) = era 0.0009 y ahora es 0.0003

CONCLUYENDO, podemos decir que la regla de 15 puntos consecutivos en la zona C es muy valiosa*, ya que puede identificar que alguna mejora ocurrió en el proceso.

* En este ejemplo, usamos el enfoque de que la causa especial fue una indicación de algo positivo, pero no siempre es así. Se puede, por ejemplo, tener un equipo de medición descalificado ocasionando mediciones con poca precisión, lo que es algo negativo, pero que también debe identificarse lo más rápido posible.