[:pb]Se vamos falar sobre análise de dados em CEP, temos que começar definindo o que é CEP:
CEP é simplesmente utilizar dados para fazer com que um conjunto de condições comporte-se da maneira desejada, a fim de obter um determinado resultado.
Utilizar dados é diferente de apenas ter dados. Já vimos no post Dados de qualidade no chão de fábrica – não os desperdice! que essas informações que coletamos no chão de fábrica tem muito a nos dizer sobre como está o andamento da produção.
Neste post queremos te explicar como funciona a análise de dados em CEP.
Para isso, vamos utilizar 2 exemplos simples
Vamos lá??
Análise de dados em CEP
O E da sigla CEP é estatístico, isso quer dizer que analisamos uma amostra representativa da nossa produção e assim conseguimos garantir a qualidade.
Quando se trata de análise de variável, acredita-se que é mais fácil, pois estamos trabalhando com números e números não mentem.
Errado!!
Como Wheeler fala no artigo Two Plus Two is Only Equal to Four on the Average, fomos criados para acreditar em números. Números são regulares, nos dão convicção.
Agora questionamos:
Dois mais dois é sempre igual a quatro?
Concorda que sempre é um termo muito forte? Podemos afirmar que dois mais dois é igual a quatro na média.
Vamos aos exemplos…
Ranking de cidades mais violentas
O Ipea e o Fórum Brasileiro de Segurança Pública fizeram uma análise, com dados de 2015, pra listar as cidades mais violentas do Brasil.
A EXAME divulgou esta lista:
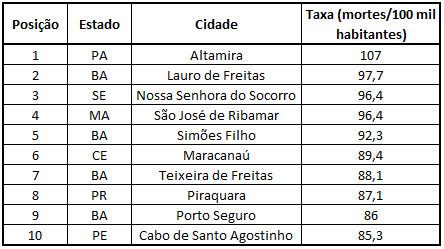 Tabela 1: Ranking das cidades mais violentas de 2015
Tabela 1: Ranking das cidades mais violentas de 2015
Essa lista considera apenas a quantidade de homicídios e MVCI (Morte Violenta por causa indeterminada) para cada 100 mil habitantes. Você acredita que esta comparação é adequada e podemos confiar totalmente nestes dados?
A Tabela 2 compara a taxa de mortalidade, apresentada na Tabela 1, com alguns outros fatores que podem influenciar.
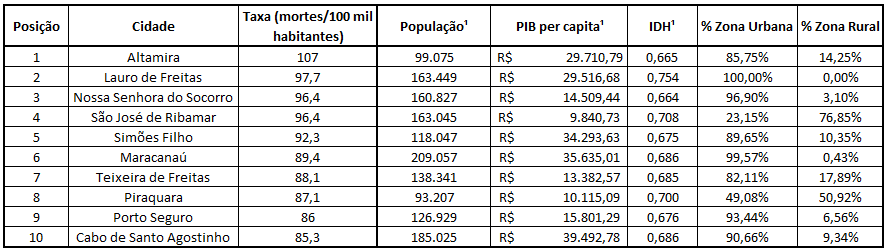 Tabela 2: Comparação da taxa de mortalidade com outros parâmetros (¹ Fonte: https://cidades.ibge.gov.br/brasil)
Tabela 2: Comparação da taxa de mortalidade com outros parâmetros (¹ Fonte: https://cidades.ibge.gov.br/brasil)
Comparando os valores de mínimo e máximo de cada parâmetro, vemos que existe diferença de:
- 124% a mais de habitantes na cidade mais populosa em comparação com a menos populosa;
- 301% a mais para o maior PIB per capita em comparação com o menor PIB per capita;
- 14% de aumento no maior IDH quando comparado com o pior IDH;
- 332% a mais da maior população que vive em Zona Urbana em relação a menor população que vive em Zona Urbana.
Com essa análise mais profunda, você acredita que a comparação apenas pela quantidade de homicídios e MVCI é adequada?
O artigo O homicídio nos municípios brasileiros confirma a relação direta entre violência e falta de escolas, hospitais públicos, concentração de renda, porte dos municípios.
Agora sabemos que apenas dividir o número de crimes registrados pela população da cidade irá inflar artificialmente a taxa de mortalidade.
O problema não é de aritmética. Não é problema de não saber manipular números, mas sim de não saber como os interpretar. Todo cálculo que já tivemos foi ensinado no mundo dos números puros. Este mundo é aquele onde as linhas não têm largura, os planos não têm espessura, e os pontos não têm dimensões!
Enquanto as coisas funcionam muito bem neste mundo de números puros, nós não vivemos lá.
Os números não são exatos no mundo em que vivemos. Eles sempre apresentam variação. Existe variação na forma como são coletados, como são analisados. Assim, sem alguma compreensão de toda essa variação, é impossível interpretar os números “desse mundo”.
Exemplo na indústria
Se um fabricante aplica dois revestimentos de filme, cada um com 2µm de espessura, podemos dizer que a espessura total será exatamente 4?
Se medirmos com cuidado e precisão suficiente (trocarmos 2 por 2,00), a espessura combinada é igual a 4 na média.
O que vemos aqui não é uma quebra nas regras da aritmética, mas uma mudança no que estamos fazendo com os números.
Ao invés de trabalhar com números puros, agora estamos usando números para caracterizar algo neste mundo. Quando fazemos isso, existe variação.
Como podemos usar números?
Quando trabalhamos com números devemos primeiro permitir a variação inerente a esses números. Isso é exatamente o que os gráficos de controle fazem – eles filtram a variação aleatória para que possamos detectar quaisquer valores excepcionais que possam estar presentes. Esta separação entre “ruído provável” e “sinais potenciais” é o objetivo de dar sentido aos dados.
Embora não seja bom perder um sinal, é igualmente ruim interpretar o ruído como se fosse um sinal. (Dica: Identifique o momento certo de ajustar o processo)
O verdadeiro truque é encontrar um equilíbrio econômico entre esses dois erros, e isso é o que Shewhart fez quando criou as cartas de controle. Esses gráficos filtram todo o ruído provável, de modo que qualquer coisa sobrando pode ser considerada como um sinal potencial.
Agora temos que escolher entre:
- Entender a variação do processo, o que facilitará o entendimento dos sinais (saber diferenciar causa aleatória de causa atribuível para prevenir problemas de desvios de qualidade)
- Ignorar a variação do processo, o que fará com que o ruído continue nos enganando.
Se nossa escolha for a primeira, podemos, enfim, concluir que “Dois mais dois é igual a quatro em média.”
Como é em média, consideramos que existe variação, por isso a importância da utilização dos Gráficos de Controle para nos auxiliar na interpretação dos dados e evitar interferência no processo sem necessidade.
* Baseado no artigo Two Plus Two is Only Equal to Four on the Average de Donald J. Wheeler.[:es]Si vamos a hablar sobre análisis de datos en SPC, tenemos que empezar definiendo lo que es SPC:
SPC es simplemente utilizar datos para hacer que un conjunto de condiciones se comporte de la manera deseada, a fin de obtener un determinado resultado.
Utilizar datos es diferente de sólo tener datos. Ya hemos visto en el post Datos de calidad en el piso de fábrica – no los desperdice! que esas informaciones que recogemos en el piso de fábrica tienen mucho que decirnos sobre cómo está el progreso de la producción.
En este post queremos explicar cómo funciona el análisis de datos en SPC.
Para ello, vamos a utilizar 2 ejemplos simples
¿¿Vamos allá??
Análisis de datos en SPC
El S de la sigla SPC es estadístico, eso quiere decir que analizamos una muestra representativa de nuestra producción y así conseguimos garantizar la calidad.
Cuando se trata de análisis de variable, se cree que es más fácil, pues estamos trabajando con números y números no mienten.
¡Malo!
Como Wheeler habla en el artículo Two Plus Two is Only Equal to Four on the Average, fuimos creados para creer en números. Los números son regulares, nos dan la convicción.
Ahora preguntamos:
¿Dos más dos es siempre igual a cuatro?
¿Concuerda que siempre es un término muy fuerte? Podemos afirmar que dos más dos es igual a cuatro en el promedio.
Vamos a los ejemplos …
Ranking de ciudades más violentas
El Ipea y el Foro Brasileño de Seguridad Pública hicieron un análisis, con datos de 2015, para listar las ciudades más violentas de Brasil.
EXAME ha publicado esta lista:
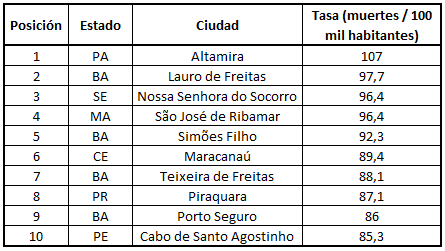 Tabla 1: Ranking de las ciudades más violentas de 2015
Tabla 1: Ranking de las ciudades más violentas de 2015
Esta lista considera sólo la cantidad de homicidios y MVCI (Muerte Violenta por causa indeterminada) por cada 100 mil habitantes. ¿Cree que esta comparación es adecuada y podemos confiar totalmente en estos datos?
La Tabla 2 compara la tasa de mortalidad, presentada en la Tabla 1, con algunos otros factores que pueden influir.
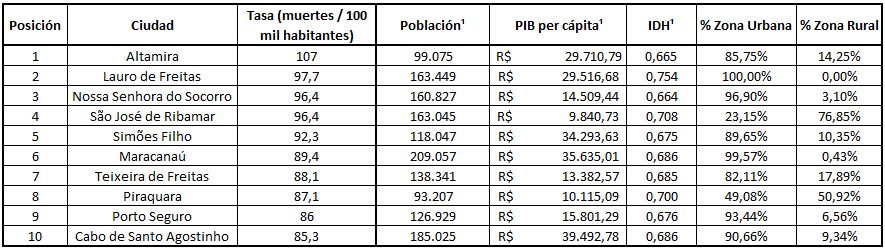 Tabla 2: Comparación de la tasa de mortalidad con otros parámetros (¹ Fuente: https://cidades.ibge.gov.br/brasil)
Tabla 2: Comparación de la tasa de mortalidad con otros parámetros (¹ Fuente: https://cidades.ibge.gov.br/brasil)
Comparando los valores de mínimo y máximo de cada parámetro, vemos que existe diferencia de:
- 124% más de habitantes en la ciudad más poblada en comparación con la menos poblada;
- 301% más para el mayor PIB per cápita en comparación con el menor PIB per cápita;
- 14% de aumento en el mayor IDH cuando comparado con el peor IDH;
- 332% más de la mayor población que vive en Zona Urbana en relación a la menor población que vive en Zona Urbana.
Con este análisis más profundo, usted cree que la comparación sólo por la cantidad de homicidios y MVCI es adecuada?
El artículo O homicídio nos municípios brasileiros (disponible sólo en portugués) confirma la relación directa entre violencia y falta de escuelas, hospitales públicos, concentración de renta, porte de los municipios.
Ahora sabemos que sólo dividir el número de crímenes registrados por la población de la ciudad va a inflar artificialmente la tasa de mortalidad.
El problema no es de aritmética. No es problema de no saber manipular números, sino de no saber cómo interpretarlos. Todo cálculo que ya tuvimos fue enseñado en el mundo de los números puros. Este mundo es aquel donde las líneas no tienen anchura, los planos no tienen espesor, y los puntos no tienen dimensiones!
Mientras las cosas funcionan muy bien en este mundo de números puros, no vivimos allí.
Los números no son exactos en el mundo en que vivimos. Ellos siempre presentan variación. Hay variación en la forma en que se recogen, como se analizan. Así, sin alguna comprensión de toda esta variación, es imposible interpretar los números “de ese mundo”.
Ejemplo en la industria
Si un fabricante aplica dos revestimientos de película, cada uno con 2μm de espesor, podemos decir que el espesor total será exactamente 4?
Si se mide con precisión y precisión (cambiamos 2 por 2,00), el espesor combinado es igual a 4 en el promedio.
Lo que vemos aquí no es una ruptura en las reglas de la aritmética, sino un cambio en lo que estamos haciendo con los números.
En lugar de trabajar con números puros, ahora estamos usando números para caracterizar algo en este mundo. Cuando lo hacemos, hay variación.
¿Cómo podemos usar números?
Cuando trabajamos con números debemos primero permitir la variación inherente a esos números. Esto es exactamente lo que las gráficas de control hacen – que filtran la variación aleatoria para que podamos detectar cualquier valor excepcional que pueda estar presente. Esta separación entre “ruido probable” y “señales potenciales” es el objetivo de dar sentido a los datos.
Aunque no es bueno perder una señal, es también malo interpretar el ruido como si fuera una señal. (Sugerencia: Identifique el momento adecuado para ajustar el proceso)
El verdadero truco es encontrar un equilibrio económico entre estos dos errores, y eso es lo que Shewhart hizo cuando creó las cartas de control. Estas gráficas filtran todo el ruido probable, de modo que cualquier cosa sobrante puede ser considerada como una señal potencial.
Ahora tenemos que elegir entre:
- Entender la variación del proceso, lo que facilitará el entendimiento de las señales (saber diferenciar causa aleatoria de causa atribuible para prevenir problemas de desvíos de calidad)
- Ignorar la variación del proceso, lo que hará que el ruido siga engañando.
Si nuestra elección es la primera, podemos, finalmente, concluir que “Dos más dos son igual a cuatro en promedio.”
Como es en promedio, consideramos que existe variación, por lo que la importancia de la utilización de las Gráficas de Control para ayudarnos en la interpretación de los datos y evitar interferencias en el proceso sin necesidad.
* Basado en el artículo Two Plus Two is Only Equal to Four on the Average de Donald J. Wheeler.[:]

![You are currently viewing [:pb]Dois mais dois NÃO é sempre igual a quatro!![:es]¡Dos más dos NO es siempre igual a cuatro !![:]](https://novosite.harbor.com.br/wp-content/uploads/2017/12/analise-de-dados-em-CEP_destaque.png)
![Read more about the article [:pb]Os Quatro Fundamentos dos Gráficos de Controle – Fundamento Dois[:es]Los Cuatro Fundamentos de las Gráficas de Control – Fundamento Dos[:]](https://novosite.harbor.com.br/wp-content/uploads/2017/04/1-fundamento-300x200.png)
![Read more about the article [:pb]Capacidade e Performance: entenda os índices Cp, Cpk, Pp e Ppk[:es]Capacidad y rendimiento: entienda los índices Cp, Cpk, Pp y Ppk[:]](https://novosite.harbor.com.br/wp-content/uploads/2017/07/indices-capacidade-300x200.png)
![Read more about the article [:pb]Dados de qualidade no chão de fábrica – não os desperdice![:es]Datos de calidad en el piso de fábrica – ¡No los desperdice![:]](https://novosite.harbor.com.br/wp-content/uploads/2017/11/imagem-destaque-blog-4-300x200.png)