[:pb]Neste post vamos falar sobre o Box Plot e como ele pode te auxiliar ainda mais na interpretação dos dados. Já discutimos em posts anteriores outras ferramentas da qualidade para análises de dados, como o Gráfico de Controle, Gráfico de Dispersão, Gráfico de Pareto e Histograma. Porém, quando queremos comparar produtos, máquinas, turnos ou lotes, a ferramenta complementar para este tipo de análise é o Box Plot.

O Box Plot é um gráfico utilizado para auxiliar na identificação de valores discrepantes de um conjunto de dados (chamados de outliers), assim como comparar a dispersão entre dois ou mais conjuntos de dados (análise da simetria). Também é bastante útil para analisar a dispersão dos conjuntos de dados em torno dos limites de especificação e do valor alvo.

Entendendo o Box Plot

Quando analisamos um conjunto de dados é usual utilizar um Histograma para entender a tendência central e a distribuição dos dados. Porém, quando desejamos comparar mais de um conjunto de dados utilizamos o Box Plot. Como podemos ver na imagem abaixo, o Histograma é a vista frontal da distribuição dos dados, enquanto o Box Plot é a vista superior de um Histograma.

O Box Plot baseia-se na localização dos quartis (quartil₁, quartil₂ ou mediana, quartil₃), que são três valores que dividem um conjunto de dados (ordenado de forma crescente) em quatro sub-intervalos, cada um com 25% das observações.

Qual o significado destes intervalos?

• 1º intervalo quartílico: é delimitado pelo Valor Mín e Q1 (quartil₁). A partir do menor ponto do conjunto de dados até o segmento vertical, encontram-se 5% dos valores do conjunto de dados; do segmento vertical até o 1º segmento do quadro amarelo, encontram-se 20% dos valores do conjunto de dados; totalizando 25% dos valores. Este intervalo é representado pelo 1º “bigode” do Box Plot.
• 2º intervalo quartílico: é delimitado pelo Q1 e Q2 (quartil₂ – mediana). Neste intervalo encontram-se mais 25% dos valores do conjunto de dados e é representado pela 1ª parte da caixa amarela.
• 3º intervalo quartílico: é delimitado pelo Q2 e Q3 (quartil₃). Neste intervalo encontram-se mais 25% dos valores do conjunto de dados e é representado pela 2ª parte da caixa amarela.
• 4º intervalo quartílico: é delimitado pelo Q3 e Valor Máx. A partir do final do quadro amarelo até o segmento vertical, encontram-se 20% dos valores do conjunto de dados; do segmento vertical ao maior ponto do conjunto de dados, encontram-se os 5% restantes dos valores do conjunto de dados, totalizando os últimos 25% dos valores. Este intervalo é representado pelo 2º “bigode” do Box plot.

Exemplo Prático

Neste exemplo vamos comparar a dispersão dos dados entre dois produtos diferentes: “Eixo Roda Dianteira” e “Eixo Roda Traseira”. A dispersão é representada pela amplitude (máximo – mínimo) dos dados, quanto maior for a amplitude, maior a variação dos dados.

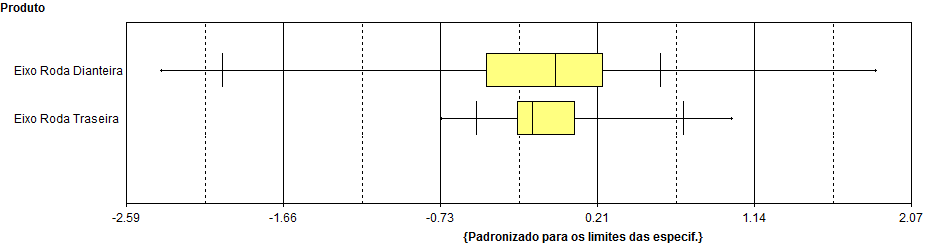
Com o Box Plot acima, conseguimos responder facilmente as seguintes questões:

• Qual é o produto que apresenta a menor variação? Eixo Roda Traseira

Este produto pode servir de exemplo para levantar as causas do processo para se obter menor variação do produto.

• Qual é o produto que apresenta a maior variação? Eixo Roda Dianteira

Por ser o produto com a maior dispersão dos dados, devemos realizar uma análise mais profunda, focada e ágil deste processo com o objetivo de diminuir a variação no produto.

Porém, onde esta variação está acontecendo?

Para enriquecer nossa análise, vamos utilizar o mesmo Box Plot adicionando mais um nível de estratificação, as características (testes) que foram avaliadas em cada peça. Três pontos diferentes (A, B e C) de diâmetros externos (DE) são avaliados para definir se a peça está conforme o padrão, respeitando seus limites de especificação.

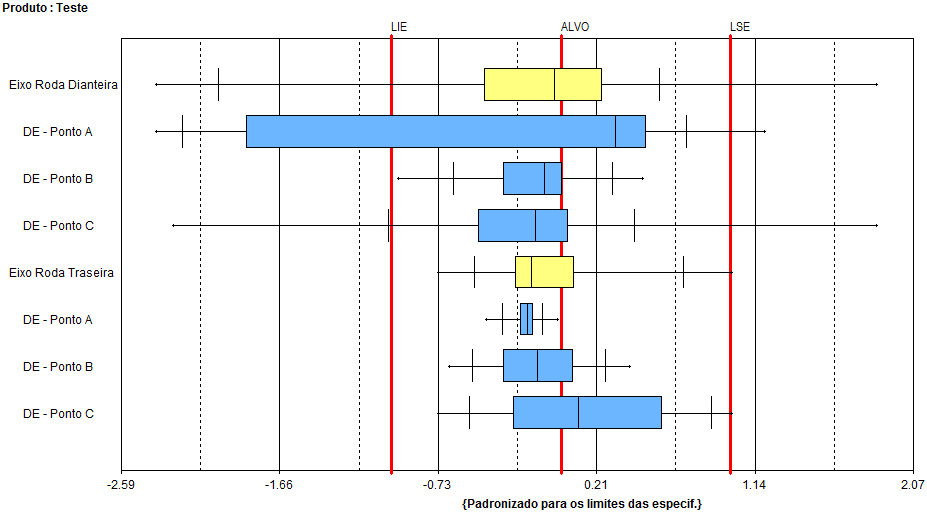
Nesta visualização do Box Plot, conseguimos ver a distribuição dos dados relacionados às características avaliadas em torno dos limites de especificação¹. De imediato, o Box Plot já nos responde as seguintes perguntas:

• Qual é a característica que apresenta a maior variação? Eixo Roda Dianteira – DE – Ponto A

Mais de 25% dos dados estão sendo produzidos fora do limite inferior de especificação (LIE), deve-se investigar mais a fundo este processo para descobrir a causa desta variação.

• Qual é a única característica dentro dos limites de especificação para o Eixo da Roda Dianteira? DE – Ponto B
  

Sua distribuição está completamente dentro dos limites de especificação. Neste caso os esforços podem ser direcionados na tentativa de centralizar a mediana do processo junto ao alvo da especificação.

• Qual característica possui os maiores bigodes? Eixo Roda Dianteira – DE – Ponto C
  

Bigodes muito grandes é um sinal de que os valores mínimo e máximo devem ser investigados. Estes pontos discrepantes são chamados de outliers e podem revelar situações como erros de medições ou de execução de procedimento. Se os dados são referentes a erros de medição, é preciso corrigi-los para que eles não interfiram na tomada de decisões. Do contrário, estes pontos podem conter informações relevantes sobre o seu processo, sendo preciso identificar a causa desta variação para que não volte a acontecer.

• Qual é a característica que apresenta a menor variação? Eixo Roda Traseira – DE – Ponto A
  

Esta é a característica onde se encontra a menor variação de todo o estudo, isto também deve ser levado em conta para entender o sucesso deste processo e tentar aplicar as mesmas condições nos demais.

O Box Plot é uma excelente ferramenta de análise que auxilia na interpretação e comparação de dados de diferentes processos, produtos, características, lotes e outros. Ele nos fornece informações à respeito da localização, dispersão e outliers do seu conjunto de dados.

Com o Software InfinityQS você consegue facilmente construir gráficos de Box Plot para a análise dos seus dados. Se sua empresa já utiliza o InfinityQS e você quer saber mais informações desse gráfico no InfinityQS, clique aqui e acesse nosso documento de suporte.

(1) Cada característica possui um limite de especificação diferente, para ser possível avaliar os limites em um mesmo gráfico os dados foram normalizados em torno do alvo especificado.

 [:es]En este post hablaremos acerca del Diagrama de Caja (Box Plot) y cómo él puede ayudarte aún más en la interpretación de los datos. Ya discutimos en posts anteriores otras herramientas de la calidad para análisis de datos, como la Gráfica de Control, Gráfica de Dispersión, Gráfica de Pareto e Histograma (disponibles sólo en portugués). Sin embargo, cuando deseamos comparar productos, máquinas, turnos o lotes, la herramienta complementaria para este tipo de análisis es el Diagrama de Caja.

El Diagrama de Caja es una gráfica utilizada para auxiliar en la identificación de valores atípicos de un conjunto de datos (llamados outliers), así como comparar la dispersión entre dos o más conjunto de datos (análisis de simetría). También es muy útil para analizar la dispersión de los conjuntos de datos alrededor de los límites de especificación y del valor objetivo.

Comprendiendo el Diagrama de Caja

Cuando analizamos un conjunto de datos es usual utilizar un Histograma para entender la tendencia central y la distribución de los datos. Sin embargo, cuando deseamos comparar más de un conjunto de datos utilizamos el Diagrama de Caja. Como vemos en la imagen abajo, el Histograma es la vista frontal de la distribución de los datos, mientras que el Diagrama de Caja es la vista superior de un histograma.

El Diagrama de Caja se basa en la localización de los cuartiles (cuartil₁, cuartil₂ o mediana, cuartil₃), que son tres valores que dividen un conjunto de datos (ordenado de manera creciente) en cuatro sub-intervalos, cada uno con el 25% de las observaciones.

¿Cuál es el significado de estos intervalos?

• 1° intervalo cuartílico: está delimitado por el Valor Mín Q1 (cuartil₁). A partir del punto más pequeño del conjunto de datos hasta el segmento vertical, se encuentra el 5% de los valores del conjunto de datos; del segmento vertical hasta el primer segmento del cuadro amarillo, se encuentra el 20% de los valores del conjunto de datos; totalizando el 25% de los valores. Este intervalo es el primer “bigote” del Diagrama de Caja.
• 2° intervalo cuartílico: está delimitado por el Q1 y Q2 (cuartil₂ – mediana). En este intervalo se encuentra el 25% de los valores del conjunto de datos y está representado por la primera parte de la caja amarilla.
• 3° intervalo cuartílico: está delimitado por el Q2 y Q3 (cuartil₃). En este intervalo se encuentra el 25% de los valores del conjunto de datos y está representado por la segunda parte de la caja amarilla.
• 4° intervalo cuartílico: está delimitado por el Q3 y Valor Máx. A partir del final de la caja amarilla hasta el segmento vertical, se encuentra el 20% de los valores del conjunto de datos; del segmento vertical al punto más grande del conjunto de datos, se encuentra el 5% restante de los valores del conjunto de datos, totalizando los últimos 25% de los valores. Este intervalo está representado por el segundo “bigote” del Diagrama de Caja.

Ejemplo Práctico

En este ejemplo vamos a comparar la dispersión de los datos entre dos productos (Partes) distintos. “Eje Rueda Delantera” y “Eje Rueda Trasera”. La dispersión es representada por el rango (máximo – mínimo) de los datos, cuanto mayor sea el rango es decir que los datos poseen mayor variación.

Con el Diagrama de Caja, imagen arriba, conseguimos responder fácilmente a las siguientes preguntas:

• ¿Cuál es el producto que presenta la menor variación? Eje Rueda Trasera

Este producto puede ser el ejemplo para conocer las causas asignables del proceso para obtener menor variación del producto.

• ¿Cuál es el producto que presenta la mayor variación? Eje Rueda Delantera

Como es el producto con la mayor dispersión de los datos, debemos realizar un análisis más profundo, enfocado y ágil de este proceso con el objetivo de disminuir la variación en el producto.

Pero, ¿dónde ocurre esta variación?

Para enriquecer nuestro análisis, vamos a utilizar el mismo Diagrama de Caja añadiendo más un nivel de estratificación, las características (pruebas) que fueran evaluadas en cada pieza. Tres puntos diferentes (A, B y C) de diámetros externos (DE) se evalúan para definir si la pieza está conforme al estándar, respetando sus límites de especificación.

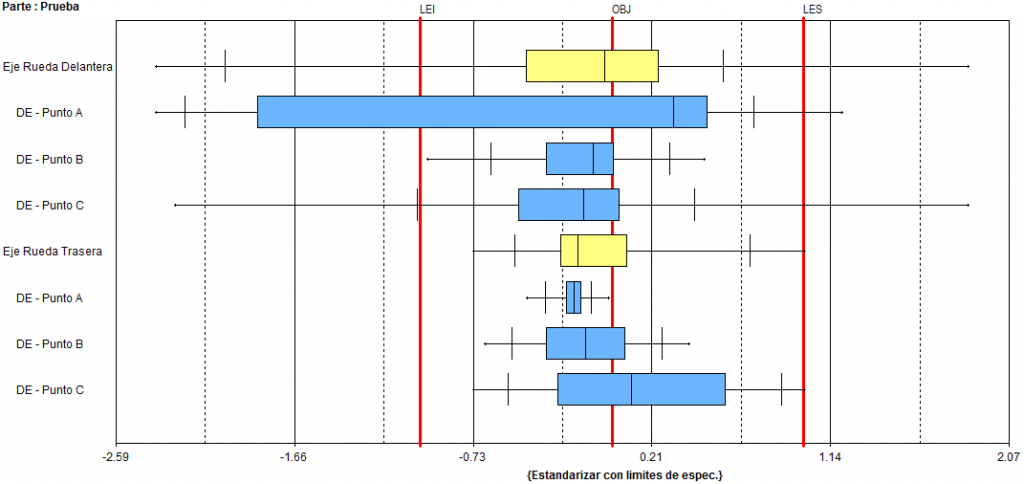
En esta visualización del Diagrama de Caja, conseguimos ver la distribución de los datos relacionados con las características evaluadas alrededor de los límites de especificación¹. De inmediato, el Diagrama de Caja ya nos responde a las siguientes preguntas:

• ¿Cuál es la característica que presenta la mayor variación? Eje Rueda Delantera – DE – Punto A

Más del 25% de los datos se producen fuera del límite de especificación inferior (LEI), se debe investigar  más a fondo el proceso para conocer las causas de esta variación.

• ¿Cuál es la única característica dentro de los límites de especificación para el Eje de la Rueda Delantera? DE – Punto B

Su distribución está completamente dentro de los límites de especificación. En este caso los esfuerzos pueden ser dirigidos en el intento de centralizar la mediana del proceso junto al objetivo de la especificación.

• ¿Cuál característica tiene el bigote más grande? Eje Rueda Delantera – DE – Punto C

Bigotes muy grandes son una señal de que los valores mínimo e máximo deben ser investigados. Estos puntos atípicos se llaman outliers, y pueden revelar errores de medición o de ejecución de procedimiento. Si los datos se refieren a errores de medición es necesario corregirlos para que no interfieran en la toma de decisiones. De lo contrario, estos puntos pueden contener información relevante acerca de tu proceso, siendo necesario identificar la causa de esta variación para que no vuelva a ocurrir.

• ¿Cuál es la característica que presenta la menor variación? Eje Rueda Trasera – DE – Punto A

Esta es la característica donde se encuentra la menor variación de todo el estudio, esto también debe ser tenido en cuenta para entender el éxito de este proceso e intentar aplicar las mismas condiciones en los otros procesos.

El Diagrama de Caja es una excelente herramienta de análisis que ayuda en la interpretación y comparación de datos de diferentes procesos, productos, características, lotes y otros. Él nos proporciona información acerca de la ubicación, dispersión y outliers de tu conjunto de datos.

Con el Software InfinityQS tu puedes fácilmente construir un Diagrama de Caja para el análisis de tus datos. Si tu empresa ya utiliza InfinityQS y deseas conocer más información de esta gráfica en InfinityQS, haga cli aquí (disponible sólo en portugués) y acceda a nuestro documento de soporte.

(1) Cada característica tiene un límite de especificación diferente, para que sea posible evaluar los límites en una misma gráfica los datos fueran estandarizados alrededor del objetivo especificado.

 [:]