[:pb]Dispersão média e desvio padrão significam a mesma coisa? O segundo Fundamento de Shewhart para os Gráficos de Controle aborda justamente esse dilema.

Fundamento Dois: Ao calcular os  limites de controle (±3 sigma), você deve SEMPRE utilizar uma estatística de dispersão média

Quando se fala em dispersão média, muitas vezes associamos ao desvio padrão, certo? Ops… mas está errado! Dispersão média e desvio padrão são estatísticas diferentes!!  Neste segundo fundamento, Shewhart enfatiza que os limites de controle (±3 sigma) devem ser calculados com base em uma estatística de dispersão média¹, que são estatísticas de dispersão dentro do subgrupo (gráfico Xbarra, n>1) ou entre os valores sucessivos (gráfico IX, n=1).

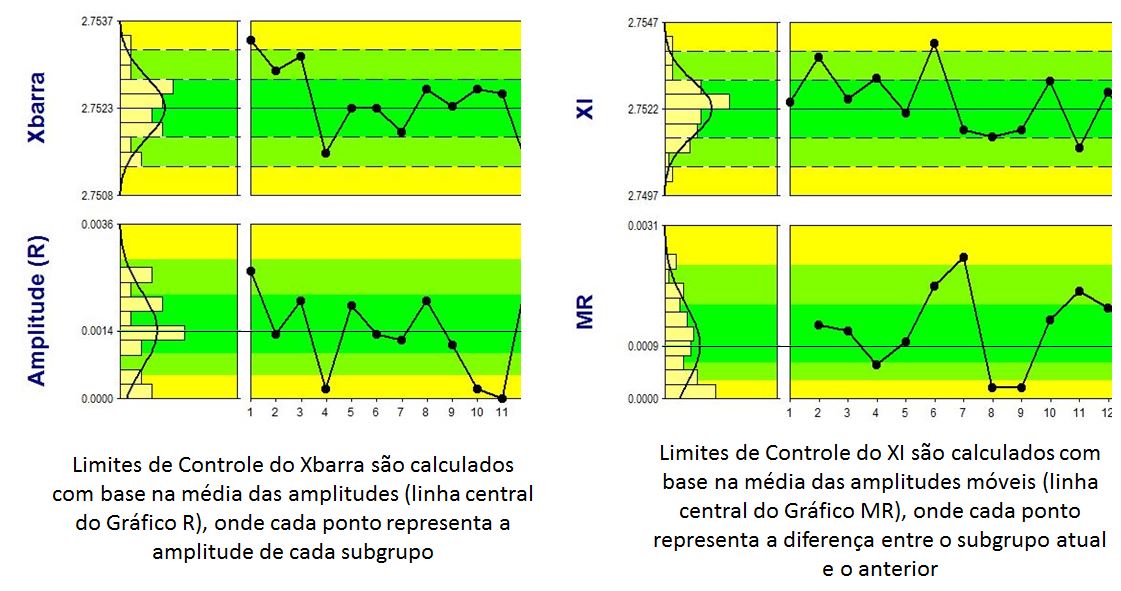
Ao utilizar uma dessas estatísticas, uma estabilidade considerável é introduzida nos cálculos dos limites. Utilizar a dispersão média dentro do subgrupo irá fornecer medidas de dispersão que são muito menos sensíveis a determinadas variações quando comparada a outras abordagens, o que diminui a probabilidade de falsos alarmes.

Ao usar uma estatística de dispersão média, aumenta-se a “robustez” do gráfico de controle. Portanto, os limites não devem ser calculados com base no desvio padrão dos indivíduos pois é mais efetivo utilizar a média das dispersões.

(1)Understanding Statistical Process Control – Donald J. Wheeler and David S. Chambers – 2010

Veja os outros fundamentos:

Fundamento Um – Utilizar limites três sigma

Fundamento Três – Definir amostragem e subgrupo racional

Fundamento Quatro – Utilizar o conhecimento adquirido

 [:es]¿La dispersión promedio y desviación estándar es la misma cosa? El Segundo Fundamento de Shewhart para las Gráficas de Control aborda precisamente este dilema.

Fundamento Dos: Al calcular los  límites de control (±3 sigma), usted deve SIEMPRE utilizar una estadística de dispersión promedio

Cuando hablamos en dispersión promedio, muchas veces hacemos la asociación con la desviación estándar, ¿verdad? Pero, no lo es cierto! Dispersión promedio y desviación estándar son estadísticas distintas!! En este segundo fundamento, Shewhart señala que los límites de control (±3 sigma) deben de ser calculados baseado en una estadística de dispersión promedio¹, que son estadísticas de dispersión dentro del subgrupo (gráfica X, n>1) o entre los valores sucesivos (gráfica XI, n=1).

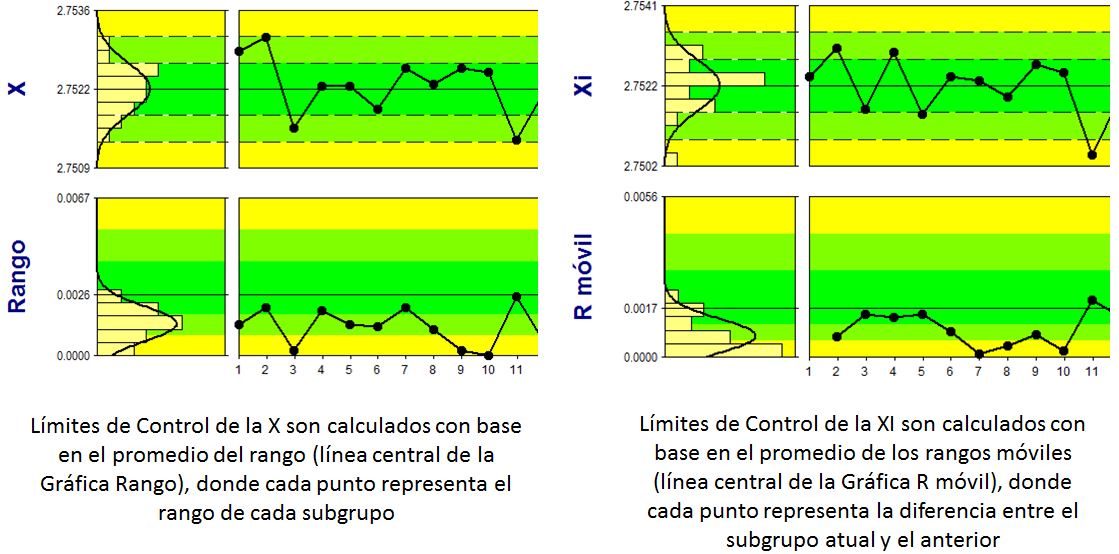
Al utilizar una de estas estadísticas se introduce   una considerable estabilidad en los cálculos de los límites. Utilizar la dispersión promedia dentro del subgrupo proporcionará medidas que son mucho menos susceptibles a ciertas variaciones en comparación con otros enfoques, lo que disminuye la probabilidad de falsas alarmas.

Mediante el uso de una estadística de dispersión promedia, se aumenta la “robustez” de la gráfica del control. Por lo tanto, los límites no deben ser calculados en base a la desviación estándar de los datos, ya que es mas eficaz utilizar el promedio de las dispersiones de los puntos de la gráfica.

(1)Understanding Statistical Process Control – Donald J. Wheeler and David S. Chambers – 2010

Vea los demás fundamentos:

Fundamento Uno – Utilizar límites tres sigma

Fundamento Tres – Definir el muestreo y el subgrupo racional

Fundamento Cuatro – Utilizar el conocimiento adquirido[:]